les algorithmes de tri sont des moyens d’organiser un tableau d’éléments du plus petit au plus grand. Ces algorithmes peuvent être utilisés pour organiser des données désordonnées et les rendre plus faciles à utiliser. De plus, avoir une compréhension de ces algorithmes et de leur fonctionnement est fondamental pour une bonne compréhension de L’informatique qui devient de plus en plus critique dans un monde de paquets préfabriqués. Ce blog se concentre sur la vitesse, les utilisations, les avantages et les inconvénients d’algorithmes de tri spécifiques.,
bien qu’il existe une grande variété d’algorithmes de tri, ce blog explique L’Insertion directe, le tri par coquille, le tri par bulle, le tri rapide, le tri par sélection et le tri par tas. Les deux premiers algorithmes (Insertion directe et Tri Shell) trient les tableaux avec insertion, c’est-à-dire lorsque les éléments sont insérés au bon endroit. Les 2 suivants (Tri à bulles et tri rapide) trient les tableaux avec échange, c’est-à-dire lorsque les éléments se déplacent dans le tableau. Le dernier est heap sort qui trie la sélection où les bons éléments sont sélectionnés lorsque l’algorithme s’exécute dans le tableau.,
Notation Big-O
avant d’aller plus loin, il est essentiel d’expliquer les méthodes utilisées par les professionnels pour analyser et évaluer la complexité et la performance des algorithmes. La norme actuelle est appelée » notation Big O « nommée d’après sa notation qui est un” O « suivi d’une fonction telle que » O(n).”
définition Formelle
Big O est utilisé pour désigner soit la complexité temporelle d’un algorithme ou de l’espace qu’il utilise. Ce blog se concentre principalement sur la partie complexité temporelle de cette notation., La façon dont les gens peuvent calculer cela est d’identifier le pire des cas pour l’algorithme ciblé et de formuler une fonction de ses performances étant donné une quantité n d’éléments. Par exemple, s’il y avait un algorithme qui recherchait le nombre 2 dans un tableau, alors le pire des cas serait si le 2 était à la toute fin du tableau. Par conséquent, la notation Big O serait O (n) car elle devrait parcourir tout le tableau à n éléments avant de trouver le nombre 2.
pour vous aider, trouvez ci-dessous un tableau avec les algorithmes et leur complexité.,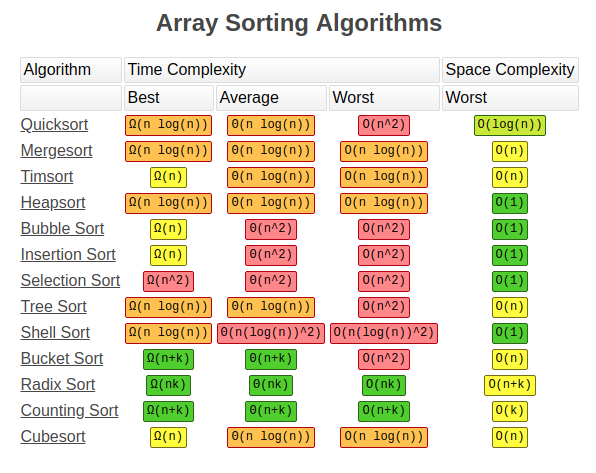
Straight Insertion Sort

Straight insertion sort est l’un des algorithmes de tri les plus élémentaires qui insère essentiellement un élément dans la bonne position d’une liste déjà triée. Il est généralement ajouté à la fin d’un nouveau tableau et se déplace vers le bas jusqu’à ce qu’il trouve un élément plus petit merci lui-même (la position souhaitée). Le processus se répète pour tous les éléments du tableau non trié. Considérons le tableau {3,1,2,5,4}, nous commençons à 3, et comme il n’y a pas d’autres éléments dans le tableau trié, le tableau trié devient juste {3}., Ensuite, nous insérons 1 qui est plus petit que 3, donc il se déplacerait devant 3 faisant le tableau {1,3}. Ce même processus est répété sur la ligne jusqu’à ce que nous obtenions le tableau {1,2,3,4,5}.
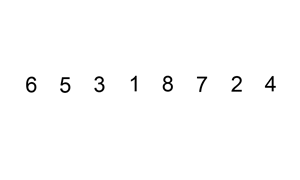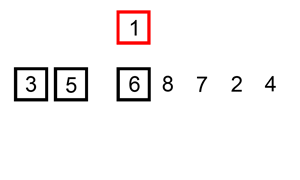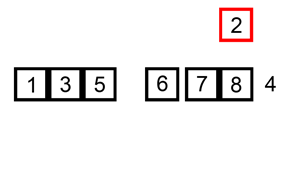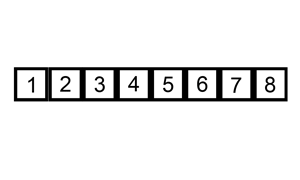
Les avantages de ce procédé est qu’il est simple et facile à mettre en œuvre. En outre, il est relativement rapide lorsqu’il y a de petites quantités d’éléments à trier. Il peut également se transformer en insertion binaire, c’est-à-dire lorsque vous comparez sur de plus longues distances et que vous l’affinez au bon endroit au lieu de comparer chaque élément au bon endroit., Cependant, un tri par insertion directe est généralement lent chaque fois que la liste devient grande.
Caractéristiques principales:
- famille de tri par Insertion
- simple et simple
- Worst case = O(n^2)
implémentation Python:
Shell Sort
Shell sort est un tri par insertion qui trie d’abord partiellement ses données en exécutant un algorithme de tri par insertion sur l’ensemble du tableau. Il commence généralement par choisir de petits sous-ensembles du tableau et trier ces tableaux., Ensuite, il répète le même processus avec des sous-ensembles plus grands jusqu’à ce qu’il atteigne un point où le sous-ensemble est le tableau, et le tout devient trié. L’avantage de faire cela est que le fait d’avoir le tableau presque entièrement trié aide le tri d’insertion final à atteindre ou à être proche de son scénario le plus efficace.
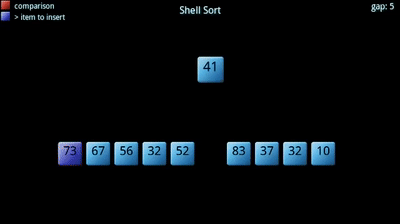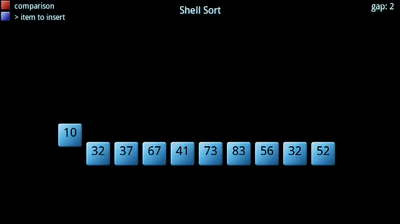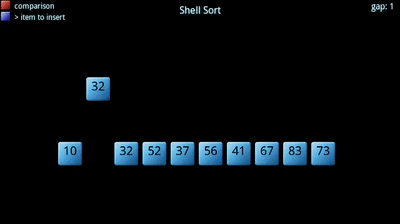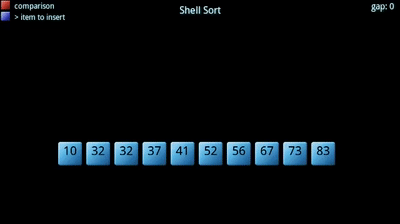
de plus, l’augmentation de la taille des sous-ensembles est obtenue par un terme d’incrément décroissant. Le terme d’incrément choisit essentiellement chaque kème élément à mettre dans le sous-ensemble., Il commence grand, conduisant à des groupes plus petits (plus étalés), et il devient plus petit jusqu’à ce qu’il devienne 1 (tout le tableau).
Le principal avantage de cet algorithme de tri est qu’il est plus efficace qu’une simple insertion de tri. En outre, il existe une variété d’algorithmes différents qui cherchent à optimiser le tri du shell en modifiant la façon dont l’incrément diminue car la seule restriction est que le dernier terme de la séquence d’incréments est 1. La plus populaire est généralement la méthode de Knuth qui utilise la formule h=((3^k) -1)/2 nous donnant une séquence d’intervalles de 1 (k=1), 4 (k=2), 13 (k=3), etc., D’autre part, le tri shell n’est pas aussi efficace que d’autres algorithmes de tri tels que quicksort et merge sort.
Caractéristiques principales:
- Tri par insertion
- peut optimiser l’algorithme en changeant les incréments
- En utilisant la méthode de Knuth, le pire des cas est O(n^(3/2))
implémentation Python:
tri des bulles
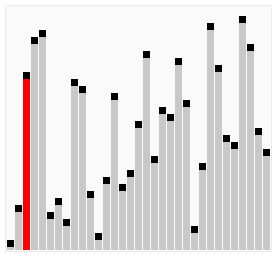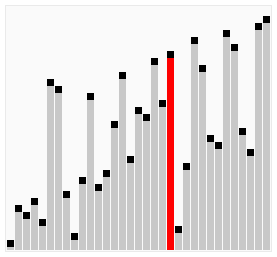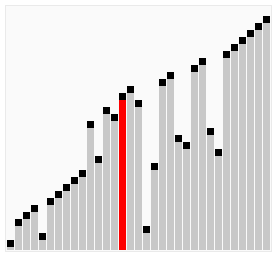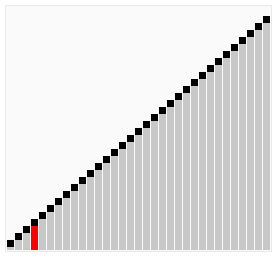
sort compare les éléments adjacents d’un tableau et organise ces éléments. Son nom vient du fait que de grands nombres ont tendance à « flotter” (bulle) vers le haut., Il parcourt un tableau et voit si le nombre à une position est supérieur au nombre dans la position suivante, ce qui entraînerait le déplacement du nombre vers le haut. Ce cycle se répète jusqu’à ce que l’algorithme ait traversé le tableau sans avoir à modifier l’ordre. Cette méthode est avantageuse car elle est simple et fonctionne très bien pour la plupart des listes triées. En conséquence, les programmeurs peuvent rapidement et facilement implémenter cet algorithme de tri. Cependant, le compromis est que c’est l’un des algorithmes de tri les plus lents.,
Caractéristiques principales:Exchange sortingfacile à implémenterworst Case = O (n ^ 2)
implémentation Python:
Quicksort
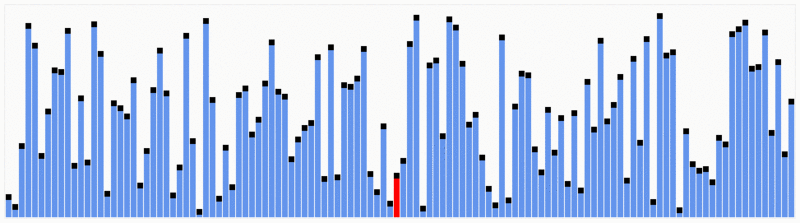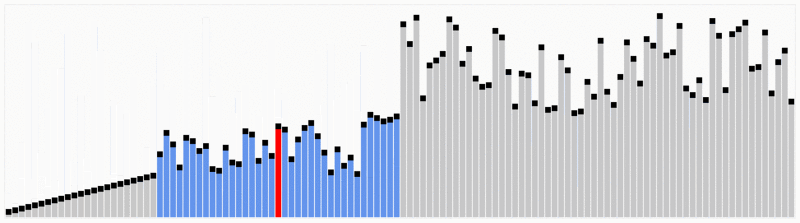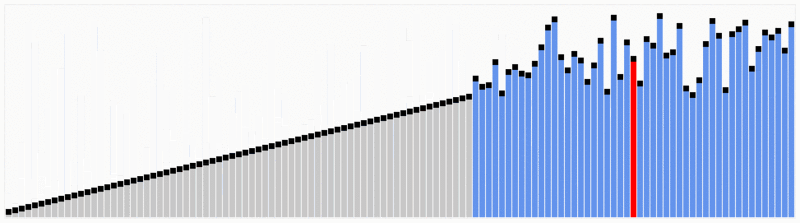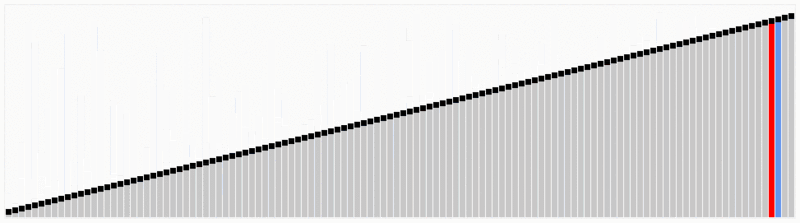
Quicksort est l’un des algorithmes de tri les plus efficaces, ce qui en fait l’un des plus utilisés.La première chose à faire est de sélectionner un numéro de pivot, ce numéro séparera les données, à sa gauche se trouvent les nombres plus petits que lui et les nombres plus grands à droite. Avec cela, nous avons divisé toute la séquence.,Une fois les données partitionnées, nous pouvons nous assurer que les partitions sont orientées, nous savons que nous avons des valeurs plus grandes à droite et des valeurs plus petites à gauche.Le quicksort utilise cet algorithme de division et de conquête avec récursivité. Donc, maintenant que nous avons les données divisées, nous utilisons la récursivité pour appeler la même méthode et passer la moitié gauche des données, et après la moitié droite pour continuer à séparer et ordonner les données. À la fin de l’exécution, nous aurons toutes les données triées.,
caractéristiques principales:
- de la famille des algorithmes de tri par échange
- diviser et conquérir le paradigme
- pire complexité O(n2)
implémentation Python:
Heapsort
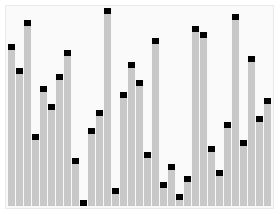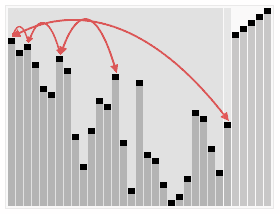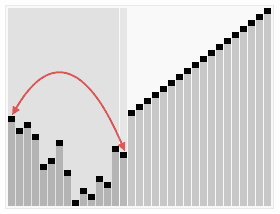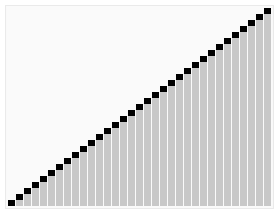
heapsort est un algorithme de tri basé sur la structure d’un tas. Le tas est une structure de données spécialisée trouvée dans un arbre ou un vector.In la première étape de l’algorithme, un arbre est créé avec les valeurs à trier, à partir de la gauche, nous créons le nœud racine, avec la première valeur., Maintenant, nous créons un nœud enfant gauche et insérons la valeur suivante, à ce moment, nous évaluons si la valeur définie sur le nœud enfant est plus grande que la valeur au nœud racine, si oui, nous changeons les valeurs. Nous faisons cela pour tous les arbres. L’idée initiale est que les nœuds parents ont toujours des valeurs plus grandes que les nœuds enfants.
à la fin de la première étape, nous créons un vecteur en commençant par la valeur racine et en marchant de gauche à droite en remplissant le vecteur.,
maintenant, nous commençons à comparer les valeurs des nœuds parents et enfants à la recherche de la plus grande valeur entre eux, et quand nous la trouvons, nous changeons de place en réorganisant les valeurs. Dans la première étape, nous comparons le nœud racine avec la dernière feuille de l’arbre. Si le nœud racine est plus grand, nous modifions les valeurs et continuons à répéter le processus jusqu’à ce que la dernière feuille soit la plus grande valeur. Quand il n’y a plus de valeurs à réorganiser, nous ajoutons la dernière feuille au vecteur et redémarrons le processus. Nous pouvons le voir dans l’image ci-dessous.,

Les principales caractéristiques de l’algorithme sont:
- De La Famille de tri par sélection
- comparaisons dans le pire des cas = O(N log n)
- Non stable
implémentation Python:
Benchmark: à quelle vitesse ils sont?
Après le développement des algorithmes, il est bon pour nous de tester à quelle vitesse ils peuvent être. Dans cette partie, nous avons développé un programme simple en utilisant le code ci-dessus pour générer une base de référence, juste pour voir combien de temps ils peuvent utiliser pour trier une liste d’entiers.,Observations importantes sur le code:
- La limite D’appel de récursivité par défaut de Python est de 1 000, dans ce test, nous utilisons de gros nombres, nous devions donc améliorer ce nombre pour exécuter le benchmark sans erreurs. La limite a été fixée à 10 000.
- ce code mesure simplement le temps d’exécution de chaque algorithme.
- Il a été fait 20 tests avec différentes tailles de listes allant de 2500 à 50000.
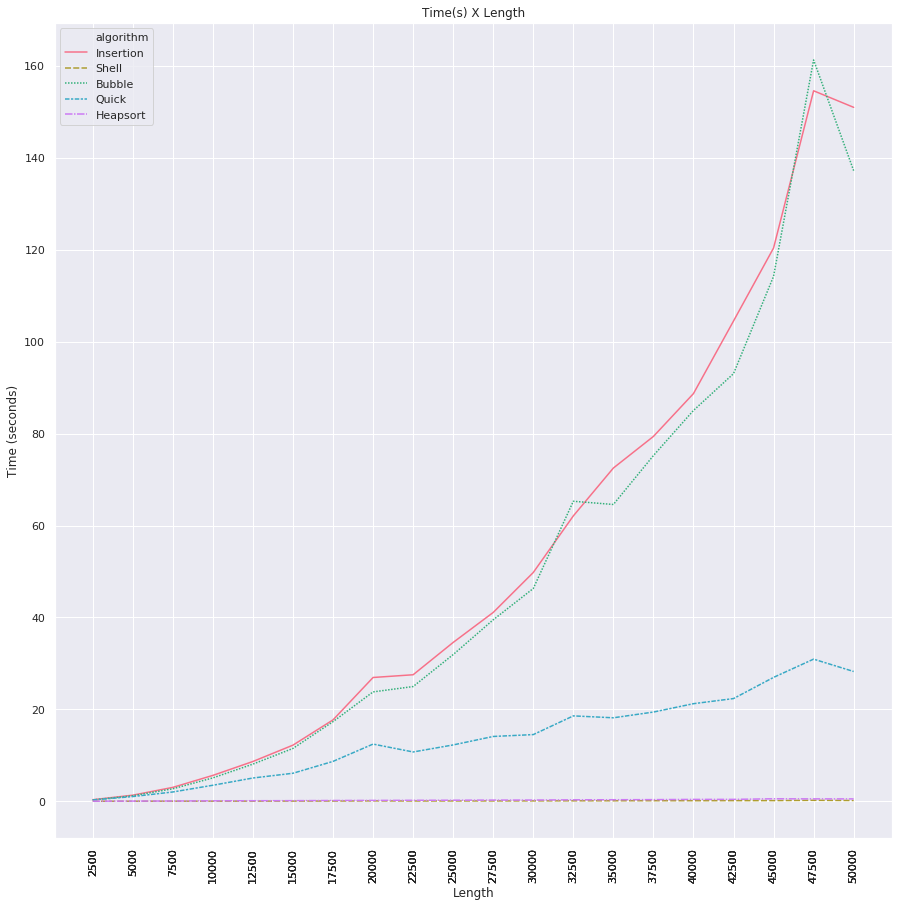
- Les nombres ont été générés randonly allant de 1 à 10000.,Les résultats sont les suivants: les algorithmes de tri Shell et de tri de tas ont bien fonctionné malgré la longueur des listes, de l’autre côté, nous avons constaté que les algorithmes de tri par Insertion et de tri par bulle étaient bien pires, augmentant largement le temps de calcul. Voir les résultats dans le tableau ci-dessous.
Conclusion
dans cet article, nous avons montré 5 des algorithmes de tri les plus courants utilisés aujourd’hui. Avant d’utiliser l’un d’eux est extrêmement important de savoir à quelle vitesse il s’exécute et l’espace dont vous allez utiliser. C’est donc le compromis entre complexité, vitesse et volume., Une autre caractéristique critique des algorithmes de tri qu’il est important de connaître est sa stabilité. La stabilité signifie que l’algorithme conserve l’ordre des éléments avec des valeurs de clé égales. Le meilleur algorithme change pour chaque ensemble de données et, par conséquent, la compréhension de nos données joue un rôle important dans le processus de choix du bon algorithme.

Comme nous pouvons le voir, la compréhension de nos données joue un rôle très important dans le processus de choix du bon algorithme.,
Si ce post a attiré votre attention, jetez un oeil à la vidéo ci-dessous, il vous donnera une explication concise sur 15 algorithmes de tri.

Big O Notation https://en.wikipedia.org/wiki/Big_O_notation
Knuth, Donald Ervin, 1938 – L’art de la programmation informatique / Donald Ervin Knuth. xiv, 782 p. 24 cm.,d= »a5b60f8536″>
Quicksort – https://commons.wikimedia.org/wiki/File:Quicksort.gif
Quicksort – http://interactivepython.org/courselib/static/pythonds/SortSearch/TheQuickSort.html
Heapsort Algorithm – https://en.wikipedia.org/wiki/Heapsort
Heapsort Algorithm – https://www.geeksforgeeks.org/heap-sort/
Bubble sort – http://interactivepython.org/runestone/static/pythonds/SortSearch/TheBubbleSort.html
Sedgewick, R.,, & Wayne, K. (2011). Algorithms, 4th Edition. (p. I–XII, 1-955). Addison-Wesley. – https://algs4.cs.princeton.edu/20sorting/
Sorting algorithms – https://brilliant.org/wiki/sorting-algorithms/