fonction de Distribution de Poisson

la distribution de Poisson fournit un moyen utile d’évaluer le pourcentage de temps pendant lequel une plage donnée de résultats sera attendue. Vous pourriez projet une limite supérieure raisonnable sur certains cas, après un certain nombre d’observations.,

par exemple, si vous n’avez mesuré un certain type d’événement spécial qu’une seule fois (x=1) au cours de votre course sur un grand accélérateur après avoir observé n événements, vous souhaiterez peut-être projeter le nombre d’événements que vous devrez observer pour avoir un niveau de confiance de 90% de voir au moins un événement spécial (Cela aiderait à défendre votre demande de plus de temps sur l’accélérateur la prochaine fois!) Ce type de projection est bien adapté aux statistiques de Poisson., Une approche pratique du calcul consiste à calculer la valeur moyenne « a » de l’observation pour laquelle l’observation de la valeur x=0 est probable à 10%. En termes de distribution de Poisson, cette condition peut être exprimée comme

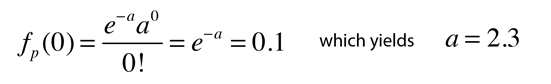
maintenant puisque la moyenne est a = n’P et la probabilité p=1/n où n est le nombre de vos observations précédentes, il s’ensuit que pour niveau de voir un autre événement spécial, vous devrez observer n’ = 2.3 n Plus d’événements. Autrement dit, vous devez observer 2.,3 fois plus que vous l’avez fait la première fois afin d’être sûr à 90% d’en voir un autre.

Une autre façon d’interpréter ce résultat est que si vous observez n événements sans voir aucun des événements spéciaux souhaités, alors avec 90% de confiance, vous pouvez dire que la valeur moyenne pour l’observation de tels événements est inférieure à 2.3 = A où a=np est la valeur moyenne standard. Basé sur un petit nombre d’observations d’événements qui sont présumés agir par pur de probabilité, vous pouvez faire une projection de la limite supérieure de ces événements à un niveau de confiance.,