Introduction to Survival Analysis: the Kaplan-Meier estimator (Français)

dans mon article précédent, j’ai décrit les cas d’utilisation potentiels de l’analyse de la survie et présenté tous les éléments nécessaires pour comprendre les techniques utilisées pour analyser les données time-to-event.

je continue la série en expliquant peut — être l’approche la plus simple, mais très perspicace de l’analyse de la survie-L’estimateur de Kaplan-Meier. Après une introduction théorique, je vais vous montrer comment effectuer l’analyse en Python en utilisant la populaire bibliothèquelifetimes.,

L’estimateur de Kaplan-Meier (également connu sous le nom d’estimateur de limite de produit, vous verrez pourquoi plus tard) est une technique non paramétrique d’estimation et de traçage de la probabilité de survie en fonction du temps. C’est souvent la première étape dans la réalisation de l’analyse de survie, comme c’est l’approche la plus simple et qui nécessite le moins d’hypothèses. Pour effectuer l’analyse en utilisant L’approche Kaplan-Meier, nous supposons ce qui suit:

• l’événement d’intérêt est sans ambiguïté et se produit à un moment clairement spécifié.,
• la probabilité de survie de toutes les observations est la même, peu importe exactement quand elles sont entrées dans l’étude.
• Les observations censurées ont les mêmes perspectives de survie que les observations qui continuent d’être suivies.

Dans les cas réels, nous ne savons jamais la véritable fonction de survie. C’est pourquoi avec L’estimateur de Kaplan-Meier, nous approximons la fonction de survie réelle à partir des données collectées.,tor est défini comme la fraction des observations qui ont survécu pendant un certain temps dans les mêmes circonstances et est donné par la formule suivante:

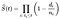
où:

• t_i est un moment où au moins un événement s’est produit,
• d_i est le nombre d’événements qui se sont produits au temps t_i,
• n_i représente le nombre d’individus connus pour avoir survécu jusqu’au temps t_i (ils n’ont pas encore eu, Ou pour le dire autrement, le nombre d’observations à risque au temps t_i.

à partir du symbole du produit dans la formule, nous pouvons voir le lien avec l’autre nom de la méthode, l’estimateur de limite de produit. La probabilité de survie au temps t est égale au produit du pourcentage de chance de survivre au temps t, et avant chaque temps.

ce que nous associons le plus souvent à cette approche de l’analyse de la survie et ce que nous voyons généralement dans la pratique sont les courbes de Kaplan-Meier — un graphique de L’estimateur de Kaplan-Meier au fil du temps., Nous pouvons utiliser ces courbes comme un outil exploratoire-pour comparer la fonction de survie entre les cohortes, les groupes qui ont reçu une sorte de traitement ou non, les groupes comportementaux, etc.

la ligne de survie est en fait une série d’étapes horizontales décroissantes, qui se rapprochent de la forme de la véritable fonction de survie de la population compte tenu d’une taille d’échantillon suffisamment importante., En pratique, le graphique est souvent accompagné d’intervalles de confiance, pour montrer à quel point nous sommes incertains quant aux estimations ponctuelles — les intervalles de confiance larges indiquent une incertitude élevée, probablement en raison de l’étude ne contenant que quelques participants — causée par la mort et la censure des observations. Pour plus de détails sur le calcul des intervalles de confiance à l’aide de la méthode de Greenwood, veuillez consulter .,

L’interprétation de la courbe de survie est assez simple, l’axe des y représente la probabilité que le sujet n’a pas connu de cas de l’intérêt après avoir survécu jusqu’à l’instant t, représentée sur l’axe des abscisses. Chaque baisse de la fonction de survie (approximée par L’estimateur de Kaplan-Meier) est causée par l’événement d’intérêt qui se produit pour au moins une observation.,

La longueur réelle de la ligne verticale représente la fraction des observations à risque qui ont vécu l’événement à l’instant t. Cela signifie qu’une seule observation (pas réellement la même, mais simplement singulière) connaissant l’événement à deux moments différents peut entraîner une baisse de la taille de la différence — en fonction du nombre d’observations à risque. De cette façon, la hauteur de la goutte peut également nous informer sur le nombre d’observations à risque (même lorsqu’elles ne sont pas déclarées et/ou qu’il n’y a pas d’intervalle de confiance).,

Lorsqu’aucune observation n’a connu l’événement d’intérêt ou que certaines observations ont été censurées, il n’y a pas de baisse de la courbe de survie.

Le test de log-rank

Nous avons appris à utiliser la méthode de Kaplan-Meier de l’estimateur à rapprocher de la véritable fonction de survie d’une population., Et nous savons que nous pouvons tracer plusieurs courbes pour comparer leurs formes, par exemple, par le système d’exploitation les utilisateurs de notre application mobile utiliser. Cependant, nous n’avons toujours pas d’outil qui permette réellement la comparaison. Eh bien, au moins un plus rigoureux que de regarder les courbes.

c’est à ce moment que le test log-rank entre en jeu. Il s’agit d’un test statistique qui compare les probabilités de survie entre deux groupes (ou plus, pour cela, veuillez consulter L’implémentation Python). L’hypothèse nulle du test indique qu’il n’existe pas de différence entre les fonctions de survie des groupes.,

le test log-rank utilise les mêmes hypothèses que l’estimateur de Kaplan-Meier. De plus, il existe l’hypothèse des dangers proportionnels — le rapport de danger (veuillez consulter l’article précédent pour un rappel sur le taux de danger) devrait être constant tout au long de la période d’étude. En pratique, cela signifie que le test log-rank pourrait ne pas être un test approprié si les courbes de survie se croisent. Cependant, c’est toujours un sujet de débat actif, veuillez voir et .

Par souci de concision, nous ne couvrons pas les mathématiques derrière le test. Si vous êtes intéressé, veuillez consulter cet article ou .,

erreurs courantes avec Kaplan-Meier

dans cette partie, je voulais mentionner certaines des erreurs courantes qui peuvent se produire en travaillant avec L’estimateur Kaplan-Meier.

suppression des DONNÉES CENSURÉES

Il pourrait être tentant de supprimer les DONNÉES CENSURÉES car cela peut modifier considérablement la forme de la courbe de Kaplan-Meier, cependant, cela peut entraîner de graves biais, nous devrions donc toujours l’inclure lors de l’ajustement du modèle.,

interprétation des extrémités des courbes

portez une attention particulière lors de l’interprétation de la fin des courbes de survie, car toute chute importante proche de la fin de l’étude ne peut s’expliquer que par quelques observations atteignant ce point de temps (cela devrait également être indiqué par des intervalles de confiance plus larges)

Dichotomisation des variables continues

par dichotomisation je veux dire utiliser la médiane ou le point de coupure « optimal” pour créer des groupes tels que « faible” et « élevé” en ce qui concerne toute métrique continue., Cette approche peut créer de multiples problèmes:

• trouver un point de coupure « optimal » peut être très dépendant de l’ensemble de données et impossible à reproduire dans différentes études. En outre, en faisant plusieurs comparaisons, nous risquons d’augmenter les chances de faux positifs (trouver une différence dans les fonctions de survie, alors qu’il n’y en a pas).
• la dichotomie diminue la puissance du test statistique en forçant toutes les mesures à une valeur binaire, ce qui peut entraîner la nécessité d’une taille d’échantillon beaucoup plus grande requise pour détecter un effet., Il convient également de mentionner qu’avec l’analyse de survie, la taille de l’échantillon requise se réfère au nombre d’observations avec l’événement d’intérêt.
• lors de la dichotomie, nous faisons de mauvaises hypothèses sur la répartition du risque entre les observations. Supposons que nous utilisons l’âge de 50 ans comme division entre les patients jeunes et âgés. Si nous le faisons, nous supposons qu’un jeune de 18 ans fait partie du même groupe à risque qu’un jeune de 49 ans, ce qui n’est pas vrai dans la plupart des cas.,

ne tenant compte que d’un seul prédicteur

L’estimateur de Kaplan-Meier est une méthode univariable, car il se rapproche de la fonction de survie en utilisant au plus une variable / prédicteur. En conséquence, les résultats peuvent être facilement biaisés-exagérant ou manquant le signal. Cela est causé par le biais dit de la variable omise, ce qui amène l’analyse à supposer que les effets potentiels de plusieurs prédicteurs ne devraient être attribués qu’à un seul, que nous prenons en compte. Pour cette raison, des méthodes multivariables telles que la régression de Cox devraient être utilisées à la place.,

exemple en Python

Il est temps d’implémenter ce que nous avons appris dans la pratique. Nous commençons par importer toutes les bibliothèques requises.

Ensuite, on charge le jeu de données et de faire quelques petites querelles pour le faire fonctionner parfaitement avec les lignes de vie de la bibliothèque. Pour l’analyse, nous utilisons le populaire jeu de données de désabonnement des clients Telco (disponible ici ou sur mon GitHub)., L’ensemble de données contient des informations sur les clients d’un fournisseur de téléphone/internet, y compris leur mandat, le type de services qu’ils utilisent, certaines données démographiques et, finalement, l’indicateur indiquant le taux de désabonnement.,

Pour cette analyse, nous utilisons les colonnes suivantes:

• tenure — le nombre de mois, le client est resté avec la société,
• churn — si le client baratté (binaire codée: 1 si l’événement qui s’est passé, 0 sinon),
• PaymentMethod— quel type de méthode de paiement les clients ont utilisé.,

pour le scénario le plus basique, nous n’avons en fait besoin que du time-to-event et du drapeau indiquant si l’événement d’intérêt s’est produit.

Le KaplanMeierFitter fonctionne de la même façon pour les classes que l’on connaît à partir de scikit-learn: nous avons d’abord instancier un objet de la classe, puis utiliser la balise fit méthode de l’ajustement du modèle aux données., Lors du traçage, nous spécifions at_risk_counts=True pour afficher en outre des informations sur le nombre d’observations à risque à certains moments.

Normalement, nous serions intéressé dans le temps de survie médian, c’est-à-point dans le temps où, en moyenne 50% de la population est déjà mort, ou dans ce cas, baratté., Nous pouvons y accéder en utilisant la ligne suivante:

kmf.median_survival_time_

cependant, dans ce cas, la commande renvoieinf, comme nous pouvons le voir sur la courbe de survie, nous n’observons pas ce point dans nos données.

Nous avons vu le cas d’utilisation de base, compliquons maintenant l’analyse et tracons les courbes de survie pour chaque variante du mode de paiement., Nous pouvons le faire en exécutant le code suivant:

en cours d’Exécution du bloc de code permet de générer les courbes ci-dessous:

Nous pouvons voir que la probabilité de survie est certainement le plus bas pour l’électronique de contrôle, tandis que les courbes automatique virement bancaire/carte de crédit sont très similaires., C’est le moment idéal pour utiliser le test log-rank pour voir s’ils sont réellement différents.

Le tableau suivant présente les résultats obtenus.

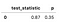
En regardant la p-valeur de 0,35, nous pouvons voir qu’il n’y a pas de raisons de rejeter l’hypothèse nulle stipulant que les fonctions de survie sont identiques. Pour cet exemple, nous n’avons comparé que deux modes de paiement., Cependant, il y a certainement plus de combinaisons que nous pourrions tester. Il existe une fonction pratique appelée pairwise_logrank_test, ce qui rend la comparaison très facile.

Dans le tableau, nous voyons la comparaison que nous avons fait, ainsi que toutes les autres combinaisons. Le virement bancaire vs., carte de crédit est le seul cas où nous ne devrions pas rejeter l’hypothèse nulle. En outre, nous devrions être prudents dans l’interprétation des résultats du test log-rank, comme nous pouvons le voir dans le graphique ci-dessus que les courbes des paiements par virement bancaire et par carte de crédit se croisent, de sorte que l’hypothèse de risques proportionnels est violée.

Il y a deux autres choses que nous pouvons facilement tester en utilisant la bibliothèque lifelines. Le premier est le test de log-rank multivarié, dans lequel l’hypothèse nulle indique que tous les groupes ont le même processus de génération de « mort”, de sorte que leurs courbes de survie sont identiques.,

les résultats de L’essai indiquent que l’on doit rejeter l’hypothèse nulle, de sorte que les courbes de survie ne sont pas identiques, ce qui, nous l’avons déjà vu dans l’intrigue.

enfin, nous pouvons tester la différence de survie à un moment précis. Pour revenir à l’exemple, dans le graphique, nous pouvons voir que les courbes sont les plus éloignées autour de t = 60., Voyons si cette différence est statistiquement significative.

En regardant les test valeur de p, il n’y a aucune raison de rejeter l’hypothèse nulle stipulant qu’il n’y a pas de différence entre la survie au moment de la commande.

Conclusions

dans cet article, j’ai décrit un outil très populaire pour effectuer une analyse de survie — l’estimateur de Kaplan-Meier., Nous avons également couvert le test log-rank pour comparer deux / plusieurs fonctions de survie. L’approche décrite est très populaire, cependant, pas sans défauts. Avant de conclure, examinons les avantages et les inconvénients de L’estimateur/courbes de Kaplan-Meier.

avantages:

• donne la vue moyenne de la population, également par groupes.
• Ne nécessite pas beaucoup de fonctionnalités — seulement les informations sur le temps de l’événement et si l’événement a réellement eu lieu. De plus, nous pouvons utiliser toutes les fonctionnalités catégorielles décrivant les groupes.,
• gère automatiquement le déséquilibre de classe, car pratiquement n’importe quelle proportion de décès par rapport aux événements censurés est acceptable.
• comme il s’agit d’une méthode non paramétrique, peu d’hypothèses sont faites sur la distribution sous-jacente des données.

inconvénients:

• nous ne pouvons pas évaluer l’ampleur de l’impact du prédicteur sur la probabilité de survie.
• nous ne pouvons pas tenir compte simultanément de plusieurs facteurs pour les observations, par exemple, le pays d’origine et le système d’exploitation du téléphone.,
• l’hypothèse de l’indépendance entre la censure et la survie (à l’instant t, les observations censurées devraient avoir le même pronostic que celles sans censure) peut être inapplicable/irréaliste.
• lorsque la distribution des données sous-jacentes est (dans une certaine mesure) connue, l’approche n’est pas aussi précise que certaines techniques concurrentes.

En résumé, même avec quelques inconvénients, les courbes de survie de Kaplan-Meier sont un excellent point de départ lors de l’analyse de la survie., Ce faisant, nous pouvons obtenir des informations précieuses sur les prédicteurs potentiels de la survie et accélérer nos progrès avec des techniques plus avancées (que je décrirai dans de futurs articles).

Vous pouvez trouver le code utilisé pour cet article sur mon GitHub. Comme toujours, toute rétroaction constructive est la bienvenue. Vous pouvez communiquer avec moi sur Twitter ou dans les commentaires.

Si vous trouvez cet article intéressant, vous pourriez aussi aimer les autres de la série:

S. Sawyer (2003)., Les intervalles de confiance de Greenwood et de Greenwood exponentiels dans L’analyse de la survie-disponibles ici

Les courbes de survie de Kaplan-Meier et le test Log-Rank — disponibles ici

risques non proportionnels-et alors? — disponible ici

Bouliotis, G.,& Billingham, L. (2011). Croisement des courbes de survie: alternatives pour le test de log-rank. Essais, 12 (S1), A137.