Déviation signifie simplement comment loin de la normale
Écart-type
L’Écart-type est une mesure de l’écart des numéros sont.
Son symbole est σ (la lettre grecque sigma)
La formule est simple: il est la racine carrée de la Variance. Alors maintenant, vous demandez: « quelle est la Variance? »
Écart
La Variance est définie comme suit:
La moyenne des carrés des écarts à la Moyenne.,
pour calculer la variance, procédez comme suit:
- Calculez la moyenne (la moyenne simple des nombres)
- puis pour chaque nombre: soustrayez la moyenne et équarrissez le résultat (la différence au carré).
- calculez ensuite la moyenne de ces différences au carré. (Pourquoi Square?)
exemple
vous et vos amis venez de mesurer les hauteurs de vos chiens (en millimètres):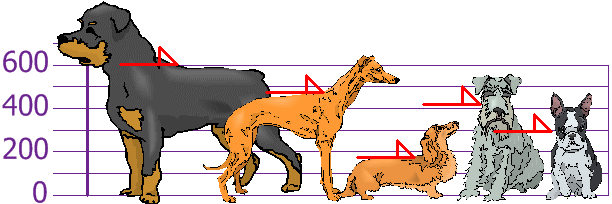
Les Hauteurs (aux épaules) sont: 600mm, 470mm, 170mm, 430mm et 300mm.,
Find out the Mean, the Variance, and the Standard Deviation.
Your first step is to find the Mean:
Answer:
| Mean | = | 600 + 470 + 170 + 430 + 3005 |
| = | 19705 | |
| = | 394 |
so the mean (average) height is 394 mm.,2062 + 762 + (−224)2 + 362 + (−94)25
So the Variance is 21,704
And the Standard Deviation is just the square root of Variance, so:
| Standard Deviation | ||
| σ | = | √21704 |
| = | 147.,32… | |
| = | 147 (le plus proche mm) | |
Et la bonne chose à propos de l’Écart-type est qu’il est utile. Maintenant, nous pouvons montrer quelles hauteurs sont dans un écart-type (147mm) de la moyenne: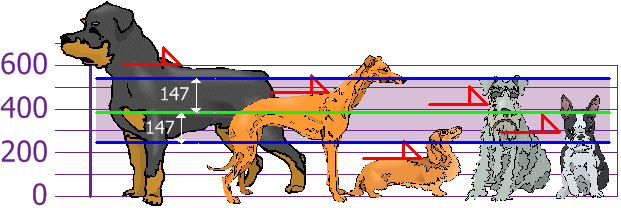
donc, en utilisant l’écart-type, nous avons une façon « standard » de savoir ce qui est normal, et ce qui est extra grand ou extra petit.
les Rottweilers sont de grands chiens. Et les teckels sont un peu courts, Non?,
en utilisant
Nous pouvons nous attendre à ce qu’environ 68% des valeurs soient dans l’écart-type plus ou moins 1.
lisez Distribution normale Standard pour en savoir plus.
essayez également le calculateur D’écart type.
Mais … il y a un petit changement avec les données de L’échantillon
notre exemple a été pour une Population (les 5 chiens sont les seuls chiens qui nous intéressent).
Mais si les données sont un échantillon (une sélection tirée d’une Population plus grande), le calcul change!,
lorsque vous avez « N » valeurs de données qui sont:
- La Population: diviser par N lors du calcul de la Variance (comme nous l’avons fait)
- Un échantillon: diviser par N-1 lors du calcul de la Variance
tous les autres calculs restent les mêmes, y compris la façon dont nous avons calculé la moyenne.,
exemple: si nos 5 chiens ne sont qu’un échantillon d’une plus grande population de chiens, nous divisons par 4 au lieu de 5 comme ceci:
formules
Voici les deux formules, expliquées dans les formules D’écart type si vous voulez en savoir plus:
|
L ‘ « écart type de Population »: |
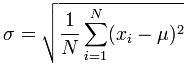 |
|
| l ‘ « écart type de l’échantillon »: | 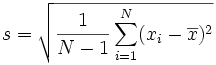 |
semble compliqué, mais le changement important est de
diviser par n-1 (au lieu de N) lors du calcul d’une variance d’échantillon.
