desvio apenas significa quão longe do Desvio-Padrão
desvio-padrão
o desvio-padrão é uma medida de como os números são distribuídos.
Seu símbolo é σ (a letra grega sigma)
a fórmula é fácil: é a raiz quadrada da variância. Pergunta-lhes: Qual é a diferença?”
variância
a variância é definida como:
a média das diferenças ao quadrado em relação à média.,
para calcular a variância siga estes passos:
- Calcule a média (a média simples dos números)
- depois para cada número: subtrai a média e quadra o resultado (a diferença ao quadrado).em seguida, calcular a média das diferenças ao quadrado. Porquê Quadrado?)
Exemplo
Você e seus amigos têm apenas mediu as alturas de seus cães (em milímetros):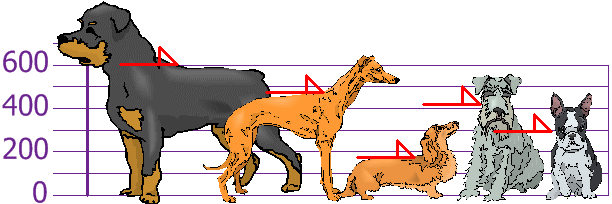
As alturas (nos ombros) são: 600mm, 470mm, 170mm, 430 mm e 300 mm.,
Find out the Mean, the Variance, and the Standard Deviation.
Your first step is to find the Mean:
Answer:
| Mean | = | 600 + 470 + 170 + 430 + 3005 |
| = | 19705 | |
| = | 394 |
so the mean (average) height is 394 mm.,2062 + 762 + (−224)2 + 362 + (−94)25
So the Variance is 21,704
And the Standard Deviation is just the square root of Variance, so:
| Standard Deviation | ||
| σ | = | √21704 |
| = | 147.,32… | |
| = | 147 (para o mais próximo mm) | |
E a coisa boa sobre o Desvio-Padrão é que ele é útil. Agora, podemos mostrar que as alturas estão dentro de um Desvio Padrão (147mm) da Média: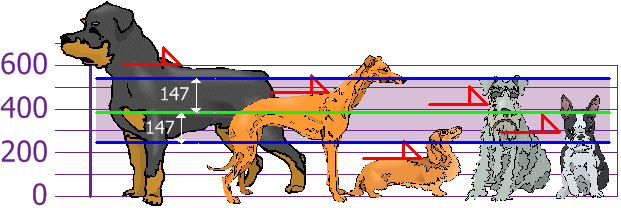
Assim, a utilização do Desvio Padrão, temos um “padrão” maneira de saber o que é normal e o que é extra grande ou muito pequeno.
Rottweilers são cães altos. E os Dachshunds são um pouco curtos, certo?,
Usando
podemos esperar cerca de 68% dos valores dentro do intervalo de mais-ou-minus1 desvio padrão.leia a distribuição Normal padrão para saber mais.
tente também a Calculadora de desvio padrão.
mas … há uma pequena mudança com dados de amostra
nosso exemplo tem sido para uma população (os 5 cães são os únicos cães em que estamos interessados).
mas se os dados são uma amostra (uma seleção tomada de uma população maior), então o cálculo muda!,
Quando você tem “N” valores de dados que são:
- População: dividir por N ao calcular a Variância (como nós fizemos)
- Um Exemplo: divisão por N-1 quando do cálculo da Variância
Todos os outros cálculos permanecer o mesmo, incluindo a forma como foi calculada a média.,
Exemplo: se nossos 5 cães são apenas uma amostra de uma população maior de cães, dividimos por 4 em vez de 5, como este:
Pense nisso como uma “correção” quando seus dados forem apenas uma amostra.,
Fórmulas
Aqui estão as duas fórmulas, explicados no Desvio Padrão Fórmulas se você quiser saber mais:
|
O “Desvio Padrão da População”: |
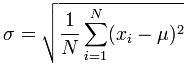 |
|
| O “Desvio Padrão da Amostra”: | 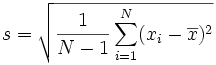 |
Parece complicado, mas o importante é
divisão por N-1 (em vez de N) ao calcular a Variância da Amostra.
