Introduction to Survival Analysis: the Kaplan-Meier estimator (Português)

No meu artigo anterior, descrevi o potencial uso-casos de análise de Sobrevivência e introduzi todos os elementos necessários para compreender as técnicas utilizadas para analisar os dados de tempo para evento.

eu continuo a série, explicando talvez a abordagem mais simples, mas muito perspicaz à análise de sobrevivência — o estimador Kaplan-Meier. Depois de uma introdução teórica, vou mostrar-lhe como realizar a análise em Python usando a popular lifetimes biblioteca.,

o estimador Kaplan-Meier (também conhecido como estimador limite de produto, você verá porque mais tarde) é uma técnica não paramétrica de estimar e traçar a probabilidade de sobrevivência como uma função do tempo. É muitas vezes o primeiro passo na realização da análise de sobrevivência, pois é a abordagem mais simples e requer os mínimos pressupostos. Para realizar a análise usando a abordagem Kaplan-Meier, assumimos o seguinte:

• o evento de interesse é inequívoco e acontece em um momento claramente especificado.,
• a probabilidade de sobrevivência de todas as observações é a mesma, não importa exatamente quando elas entraram no estudo.as observações censuradas têm as mesmas perspectivas de sobrevivência que as observações que continuam a ser seguidas.

em casos reais, nunca conhecemos a verdadeira função de sobrevivência. É por isso que com o estimador Kaplan-Meier, nós aproximamos a verdadeira função de sobrevivência a partir dos dados coletados.,tor é definido como a fração de observações que sobreviveu durante um determinado período de tempo, sob as mesmas circunstâncias, e é dado pela seguinte fórmula:

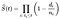
, onde:

• t_i é um momento em que pelo menos um evento aconteceu,
• d_i é o número de eventos que aconteceram no tempo t_i,
• n_i representa o número de pessoas que se sabe terem sobrevivido até ao momento de t_i (eles ainda não teve a morte do evento ou que tenham sido censurado)., Ou, dito de forma diferente, o número de observações em risco no momento t_i.

do símbolo do produto na fórmula, podemos ver a conexão com o outro nome do método, o estimador limite de produto. A probabilidade de sobrevivência no momento t é igual ao produto da percentagem de probabilidade de sobrevivência no momento t e em cada momento anterior.

O que mais frequentemente associamos com esta abordagem à análise de Sobrevivência e o que geralmente vemos na prática são as curvas Kaplan-Meier — um gráfico do estimador Kaplan-Meier ao longo do tempo., Podemos usar essas curvas como uma ferramenta exploratória — para comparar a função de sobrevivência entre coortes, grupos que receberam algum tipo de tratamento ou não, Grupos comportamentais, etc.

a linha de sobrevivência é na verdade uma série de passos horizontais decrescentes, que se aproximam da forma da verdadeira função de sobrevivência da população, dado um tamanho suficiente de amostra., Na prática, o enredo é muitas vezes acompanhado por intervalos de confiança, para mostrar o quão incertos estamos sobre as estimativas de pontos — intervalos de confiança em toda a parte indicam alta incerteza, provavelmente devido ao Estudo contendo apenas alguns participantes — causado por ambas as observações morrer e ser censurado. Para mais detalhes sobre o cálculo dos intervalos de confiança usando o método Greenwood, por favor veja .,

A interpretação da curva de sobrevivência é bastante simples, o eixo y representa a probabilidade de que o assunto ainda não experimentou o evento de interesse depois de sobreviver até o tempo t, representado no eixo x. Cada queda na função de sobrevivência (aproximada pelo estimador Kaplan-Meier) é causada pelo evento de interesse acontecendo por pelo menos uma observação.,

O comprimento real da linha vertical representa a fração de observações em situação de risco que ocorreu o evento no tempo t. Isso significa que uma única observação (na verdade, não o mesmo, mas simplesmente singular) enfrentando o evento em dois momentos diferentes pode resultar em uma queda da diferença de tamanho, dependendo do número de observações em risco. Desta forma, a altura da queda também pode nos informar sobre o número de observações em risco (mesmo quando não relatadas e/ou não há intervalos de confiança).,quando nenhuma observação experimentou o evento de interesse ou algumas observações foram censuradas, não há queda na curva de sobrevivência.

O teste log-rank

Nós aprendemos como usar a turbina de Kaplan-Meier estimador para aproximar a verdadeira função de sobrevivência de uma população., E sabemos que podemos plotar várias curvas para comparar suas formas, por exemplo, pelo SO os usuários de nosso aplicativo móvel. No entanto, ainda não dispomos de um instrumento que permita efectivamente a comparação. Bem, pelo menos um mais rigoroso do que olhar para as curvas.

é quando o teste log-rank entra em jogo. É um teste estatístico que compara as probabilidades de sobrevivência entre dois grupos (ou mais, por favor veja a implementação em Python). A hipótese nula do teste afirma que não há diferença entre as funções de sobrevivência dos grupos considerados.,o teste log-rank utiliza os mesmos pressupostos do estimador Kaplan-Meier. Além disso, existe a hipótese proporcional de perigos — a razão de perigo (ver o artigo anterior para um lembrete sobre a taxa de perigo) deve ser constante ao longo do período de estudo. Na prática, isto significa que o teste log-rank pode não ser um teste adequado se as curvas de sobrevivência se cruzarem. No entanto, este é ainda um tema de debate activo, por favor, veja e .

para brevidade, não cobrimos a matemática por trás do teste. Se você estiver interessado, por favor Veja este artigo ou .,nesta parte, eu queria mencionar alguns dos erros comuns que podem ocorrer durante o trabalho com o estimador Kaplan-Meier.

remover dados censurados

pode ser tentador remover dados censurados uma vez que pode alterar significativamente a forma da curva Kaplan-Meier, no entanto, isso pode levar a vieses graves, por isso devemos sempre incluí-lo ao encaixar o modelo.,

Interpretar as extremidades das curvas

Preste especial atenção ao interpretar o fim das curvas de sobrevida, como grandes gotas de perto a final do estudo, pode ser explicado por apenas algumas observações de chegar a este ponto de tempo (isto também deve ser indicado pelo maior intervalo de confiança)

Dichotomizing variáveis contínuas

Por dichotomizing quero dizer, usando a mediana ou “ideal” ponto de corte para criar grupos, tais como “baixa” e “alta” em relação a qualquer contínua métrica., Esta abordagem pode criar vários problemas:

• encontrar um ponto de corte” ideal ” pode ser muito dependente do conjunto de dados e impossível de replicar em diferentes estudos. Além disso, ao fazer comparações múltiplas, corremos o risco de aumentar as chances de falsos positivos (encontrando uma diferença nas funções de sobrevivência, quando na verdade não há nenhuma).
• Dicotomizar diminui a potência do teste estatístico forçando todas as medições a um valor binário, o que por sua vez pode levar à necessidade de um tamanho de amostra muito maior necessário para detectar um efeito., Vale ressaltar também que, com a análise de sobrevivência, o tamanho requerido da amostra refere-se ao número de observações com o evento de interesse.quando dicotomizamos, fazemos más suposições sobre a distribuição do risco entre as observações. Vamos supor que usamos a idade de 50 anos como a divisão entre pacientes jovens e idosos. Se o fizermos, partimos do princípio de que um jovem de 18 anos está no mesmo grupo de risco que um jovem de 49 anos, o que não é verdade na maioria dos casos.,

contabilizando apenas um predictor

o estimador Kaplan-Meier é um método univariável, uma vez que se aproxima da função de sobrevivência usando no máximo uma variável / predictor. Como resultado, os resultados podem ser facilmente tendenciosos-ou exagerando ou perdendo o sinal. Isso é causado pelo chamado viés variável omitido, que faz com que a análise assuma que os efeitos potenciais de múltiplos predictores devem ser atribuídos apenas ao único, que levamos em conta. Por causa disso, métodos multivariáveis, como a regressão Cox deve ser usado em vez disso.,

exemplo em Python

É hora de implementar o que aprendemos na prática. Começamos por importar todas as bibliotecas necessárias.

Depois, carregamos o conjunto de dados e fazemos algumas pequenas discussões para que funcione bem com a biblioteca lifelines. Para a análise, utilizamos o popular conjunto de dados Churn do cliente Telco (disponível aqui ou no meu GitHub)., O conjunto de dados contém informações dos clientes de um fornecedor de telefone / internet, incluindo o seu mandato, que tipo de serviços utilizam, alguns dados demográficos e, em última análise, a bandeira que indica o churn.,

Para esta análise, utilizamos as seguintes colunas:

• tenure — o número de meses em que o cliente tiver permanecido com a empresa,
• churn — a informação se o cliente batido (binário codificado em: 1 se o evento aconteceu, 0 caso contrário),
• PaymentMethod— que tipo de método de pagamento utilizado pelo cliente.,

para o cenário mais básico, na verdade só precisamos do tempo para o evento e da bandeira indicando se o evento de interesse aconteceu.

KaplanMeierFitter funciona da mesma forma para as classes conhecidas de scikit-learn: primeiro iremos instanciar o objeto da classe e, em seguida, use o fit método para ajustar o modelo aos nossos dados., Enquanto plotamos, especificamos at_risk_counts=True para adicionalmente exibir informações sobre o número de observações em risco em certos pontos do tempo.

Normalmente, nós estamos interessados na mediana do tempo de sobrevivência, isto é, o ponto no tempo em que, em média, 50% da população já morreu, ou, neste caso, batido., Podemos acessá-lo usando a seguinte linha:

kmf.median_survival_time_

no Entanto, neste caso, o comando retorna inf, como podemos ver a partir da curva de sobrevivência que nós realmente não observar que ponto, em nossos dados.

vimos o caso de uso básico, agora vamos complicar a análise e traçar as curvas de sobrevivência para cada variante do método de pagamento., Podemos fazer isso executando o código a seguir:

a Executar o bloco de código gera a seguinte trama:

Podemos ver que a probabilidade de sobrevivência é, definitivamente, o mais baixo para o cheque eletrônico, enquanto as curvas do sistema automático de transferência bancária/cartão de crédito são muito semelhantes., Este é um momento perfeito para usar o teste log-rank para ver se eles são realmente diferentes.

a tabela A seguir apresenta os resultados.

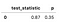
observando o p-valor igual a 0,35, podemos ver que não há razões para rejeitar a hipótese nula, indicando que a sobrevivência funções são idênticas. Por exemplo, comparámos apenas dois métodos de pagamento., No entanto, há definitivamente mais combinações que podemos testar. Há uma função útil chamada pairwise_logrank_test, o que torna a comparação muito fácil.

Na tabela, vemos que a anterior comparação que fizemos, assim como todas as outras combinações. The bank transfer vs., o cartão de crédito é o único caso em que não devemos rejeitar a hipótese nula. Além disso, devemos ser cautelosos sobre como interpretar os resultados do teste log-rank, como podemos ver no gráfico acima que as curvas para a transferência bancária e de pagamentos de cartão de crédito realmente cruz, então, a suposição de riscos proporcionais é violada.

Existem mais duas coisas que podemos testar facilmente usando a biblioteca lifelines. O primeiro é o teste de log-rank multivariado, no qual a hipótese nula afirma que todos os grupos têm o mesmo processo gerador de “morte”, de modo que suas curvas de sobrevivência são idênticas.,

Os resultados do teste indicam que devemos rejeitar a hipótese nula, de modo que as curvas de sobrevida não são idênticas, o que já vimos na trama.por último, podemos testar a diferença de sobrevivência num determinado momento. Voltando ao exemplo, no gráfico, podemos ver que as curvas estão mais afastadas em torno de T = 60., Vamos ver se essa diferença é estatisticamente significativa.

observando o teste do p-valor, não há nenhuma razão para rejeitar a hipótese nula, indicando que não há diferença entre a sobrevivência em que ponto do tempo.

conclusões

neste artigo, descrevi uma ferramenta muito popular para a realização da análise de sobrevivência — o estimador Kaplan-Meier., Também cobrimos o teste log-rank para comparar duas / múltiplas funções de sobrevivência. A abordagem descrita é muito popular, no entanto, não sem falhas. Antes de concluir, vamos dar uma olhada nos prós e contras do estimador/curvas Kaplan-Meier.vantagens:

• dá a visão média da população, também por grupos.
• não requer um monte de recursos — apenas a informação sobre o tempo para o evento e se o evento realmente ocorreu. Além disso, podemos usar todas as características categóricas que descrevem grupos.,
• automaticamente lida com desequilíbrio de classe, como virtualmente qualquer proporção de morte para eventos censurados é aceitável.
• Como é um método não paramétrico, poucas suposições são feitas sobre a distribuição subjacente dos dados.

desvantagens:

• não podemos avaliar a magnitude do impacto do predictor na probabilidade de sobrevivência.
• não podemos simultaneamente explicar múltiplos fatores para observações, por exemplo, o país de origem e o sistema operacional do telefone.,
• a suposição da independência entre censurar e sobrevivência (no momento t, observações censuradas devem ter o mesmo prognóstico que as sem censurar) pode ser inaplicável/irrealista.quando a distribuição de dados subjacente é (até certo ponto) conhecida, a abordagem não é tão precisa como algumas técnicas concorrentes.

resumindo, mesmo com algumas desvantagens as curvas de sobrevivência Kaplan-Meier são um ótimo lugar para começar enquanto se realiza a análise de sobrevivência., Ao fazê-lo, podemos obter informações valiosas sobre os potenciais preditores de Sobrevivência e acelerar o nosso progresso com algumas técnicas mais avançadas (que vou descrever em artigos futuros).

pode encontrar o código usado para este artigo no meu GitHub. Como sempre, qualquer feedback construtivo é bem-vindo. Pode contactar – me no Twitter ou nos comentários.

no caso de você achar este artigo interessante, Você também pode gostar dos outros da série:

S. Sawyer (2003)., Os intervalos de confiança em Greenwood E Greenwood exponencial na análise de Sobrevivência — disponíveis aqui nas curvas de sobrevivência de Kaplan-Meier e no teste Log-Rank-disponíveis aqui em

perigos Não proporcionais — e daí? – available here

Bouliotis, G., & Billingham, L. (2011). Curvas de sobrevivência de cruzamento: alternativas ao teste log-rank. Trials, 12 (S1), A137.