Poisson Distribution Function

The Poisson distribution provides a useful way to assess the percentage of time when a given range of results will be expected. Você pode querer projetar um limite máximo razoável em algum evento depois de fazer uma série de observações.,

Por exemplo, se medir um determinado tipo de evento especial, apenas uma vez (x=1) durante a sua execução em um grande acelerador, depois de observar eventos de n, então você pode querer projeto de quantos eventos você teria que observar a 90% de nível de confiança de ver pelo menos um de tais eventos especiais. (Isso ajudaria a defender o seu pedido de mais tempo no acelerador da próxima vez!) Este tipo de projeção é bem adequado para as estatísticas de Poisson., Uma abordagem conveniente para o cálculo é calcular o valor médio ” a ” da observação para a qual a observação do valor x=0 é 10% provável. Em termos da distribuição de Poisson, esta condição pode ser expressa como:

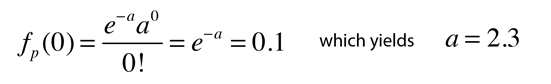
Agora, uma vez que a média é de a = n’p e a probabilidade p=1/n, onde n é o número de observações anteriores, segue-se que para atingir 90% de nível de confiança de ver outro evento especial, você teria que observar n’ = 2.3 n mais eventos. Isto é, você deve observar 2.,Três vezes mais do que você fez a primeira vez, a fim de ter 90% de certeza de ver outro.

Outra forma de interpretar este resultado é que, se você observar eventos de n sem ver qualquer um dos desejado eventos especiais, então com 90% de confiança, pode-se dizer que o valor médio para a observação de tais eventos é menor que 2,3 = a, onde a=np é o padrão do valor médio. Com base em um pequeno número de observações de eventos que se presume que atuam por pura probabilidade, você pode fazer uma projeção do limite superior para tais eventos em um nível escolhido de confiança.,