resolver equações polinomiais de ordem superior é uma habilidade essencial para qualquer um estudando ciência e matemática. No entanto, compreender como resolver este tipo de equações é bastante desafiador.
neste artigo, vamos aprender como resolver as equações cúbicas usando diferentes métodos como o método de divisão, Teorema do fator e factoring por agrupamento.
mas antes de entrar neste tópico, vamos discutir o que é uma equação polinomial e cúbica.,
um polinômio é uma expressão algébrica com um ou mais termos em que uma constante e uma variável são separadas por uma adição ou um sinal de subtração.
a forma geral de um polinômio é axn + bxn – 1 + cxn-2 +…. + kx + l, onde cada variável tem uma constante que o acompanha como seu coeficiente. Os diferentes tipos de polinômios incluem: binômios, trinômios e quadrinômios. Exemplos de polinômios são: 3x + 1, x2 + 5xy – ax-2AY, 6×2 + 3x + 2x + 1 etc.uma equação cúbica é uma equação algébrica de terceiro grau.,a forma geral de uma função cúbica é: f (x) = ax3 + bx2 + cx1 + D. e a equação cúbica tem a forma de ax3 + bx2 + cx + d = 0, onde a, b E c são os coeficientes e d é a constante.
como resolver equações cúbicas?
a maneira tradicional de resolver uma equação cúbica é reduzi-la a uma equação quadrática e então resolvê-la por fatoração ou fórmula quadrática.como uma equação quadrática tem duas raízes reais, uma equação cúbica pode ter possivelmente três raízes reais., Mas ao contrário da equação quadrática que pode não ter solução real, uma equação cúbica tem pelo menos uma raiz real.as outras duas raízes podem ser reais ou imaginárias.
sempre que lhe é dada uma equação cúbica, ou qualquer equação, você sempre tem que organizá-la em uma forma padrão primeiro.
Por exemplo, se lhe for dado algo assim, 3×2 + x-3 = 2 / x, você irá re-organizar no formulário padrão e escrevê – lo como, 3×3 + x2 – 3x-2 = 0. Então você pode resolver isso por qualquer método adequado.,
Vamos ver alguns exemplos para melhor compreensão:
Exemplo 1
Determinar as raízes da equação cúbica 2×3 + 3×2 – 11x – 6 = 0
Solução
Desde que d = 6 e, em seguida, os possíveis fatores são: 1, 2, 3 e 6.
agora aplique o Teorema do fator para verificar os valores possíveis por tentativa e erro.
f (1) = 2 + 3 – 11 – 6 ≠ 0
f (-1) = -2 + 3 + 11 – 6 ≠ 0
f (2) = 16 + 12 – 22 – 6 = 0
Portanto, x = 2 é o primeiro de raiz.
portanto, as soluções São x = 2, x = -1 / 2 e x = -3.,
Exemplo 2
Encontrar as raízes da equação cúbica x3 − 6×2 + 11x – 6 = 0
Solução
x3 − 6×2 + 11x – 6
(x – 1) é um dos fatores.
dividindo x3 − 6×2 + 11x – 6 (x – 1),
⟹ (x – 1) (x2 – 5x + 6) = 0
⟹ (x – 1) (x – 2) (x – 3) = 0
Este da equação cúbica soluções são x = 1, x = 2 e x = 3.
Exemplo 3
Resolver x3 – 2×2 – x + 2
Solução
Factorizar a equação.
x3 – 2×2 – x + 2 = x2(x – 2) (x – 2)
= (x2 – 1) (x – 2)
= (x + 1) (x – 1) (x – 2)
x = 1, -1 e 2.,
Example 4
Solve the cubic equation x3 – 23×2 + 142x – 120
Solution
First factorize the polynomial.
x3 – 23×2 + 142x – 120 = (x – 1) (x2 – 22x + 120)
But x2 – 22x + 120 = x2 – 12x – 10x + 120
= x (x – 12) – 10(x – 12)
= (x – 12) (x – 10)
Therefore, x3 – 23×2 + 142x – 120 = (x – 1) (x – 10) (x – 12)
Equate each factor to zero.
x – 1= 0
x = 1
x – 10 = 10
x – 12= 0
x = 12
The roots of the equation are x = 1, 10 and 12.
Example 5
Solve the cubic equation x3 – 6 x2 + 11x – 6 = 0.,
Solução
Para resolver este problema usando o método de divisão, tomar qualquer fator de constante 6;
let x = 2
Dividir o polinômio por x-2
(x2 – 4x + 3) = 0.
Agora resolver a equação quadrática (x2 – 4x + 3) = 0 para obter x= 1 ou x = 3
Portanto, as soluções são x = 2, x= 1 e x =3.
Exemplo 6
Resolver a equação cúbica x3 – 7×2 + 4x + 12 = 0
Solução
seja f(x) = x3 – 7×2 + 4x + 12
Desde que d = 12, os valores possíveis são 1, 2, 3, 4, 6 e 12.,por tentativa e erro, descobrimos que (-1) = -1 – 7 – 4 + 12 = 0
assim, (x + 1) é um fator da função.
x3 – 7×2 + 4x + 12
= (x + 1) (x2 – 8x + 12)
= (x + 1) (x – 2) (x – 6)
Portanto, x = -1, 2, 6
Exemplo 7
Resolver a seguinte equação cúbica:
x3 + 3×2 + x + 3 = 0.
Solução
x3 + 3×2 + x + 3
= (x3 + 3×2) + (x + 3)
= x2(x + 3) + 1(x + 3)
= (x + 3) (x2 + 1)
Portanto, x = -1 ,1 -3.,
Example 8
Solve x3 − 6×2 + 11x − 6 = 0
Solution
Factorize
x3 − 6×2 + 11x − 6 = 0 ⟹ (x − 1) (x − 2) (x − 3) = 0
Equating each factor to zero gives;
x = 1, x = 2 and x = 3
Example 9
Solve x 3 − 4×2 − 9x + 36 = 0
Solution
Factorize each set of two terms.,ing cada fator para zero, temos;
x = -3, 3 ou 4
por Exemplo, 10
Resolver a equação 3×3 −16×2 + 23x − 6 = 0
Solução
Dividir 3×3 −16×2 + 23x – 6 x -2 para obter 3×2 – 1x – 9 x + 3
= x (3x – 1) – 3(3x – 1)
= (x – 3) (3x – 1)
Portanto, 3×3 −16×2 + 23x − 6 = (x – 2) (x – 3) (3x – 1)
Equacionar cada fator a zero para obter,
x = 2, 3 e 1/3
Exemplo 11
Encontrar as raízes de 3×3 – 3×2 – 90x=0
Solução
fator é 3x
3×3 – 3×2 – 90x ⟹3x (x2 – x – 30)
de Encontrar um par de fatores cujo produto é -30 e a soma é-1.,
⟹- 6 * 5 =-30
⟹ -6 + 5 = -1
reescrever a equação substituindo o termo “bx” pelos fatores escolhidos.
⟹ 3x
Fator da equação;
⟹ 3x
= 3x (x – 6) (x + 5)
Por equivalendo cada fator para zero, temos;
x = 0, 6, -5
de Resolução de equações cúbicas usando o método gráfico
Se você não conseguir resolver a equação cúbica por qualquer um dos métodos acima, você pode resolvê-lo graficamente. Para isso, você precisa ter um esboço preciso da equação cúbica dada.,
O (S) ponto (s) onde o seu grafo atravessa o eixo x, é uma solução da equação. O número de soluções reais das equações cúbicas é o mesmo que o número de vezes que seu grafo cruza o eixo x.
exemplo 12
encontrar as raízes de x3 + 5×2 + 2x – 8 = 0 graficamente.
Solução
Basta desenhar o gráfico da seguinte função substituindo-se valores aleatórios de x:
f (x) = x3 + 5×2 + 2x – 8
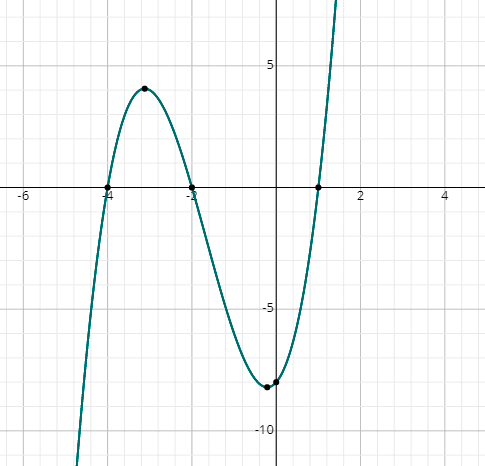
Você pode ver o gráfico corta o eixo x em 3 pontos, portanto, existem 3 soluções reais.,
do Gráfico, as soluções são:
x = 1, x = -2 & x = -4.
Questões Práticas
resolver as seguintes equações cúbicas: