résoudre des équations polynomiales d’ordre supérieur est une compétence essentielle pour quiconque étudie les sciences et les mathématiques. Cependant, comprendre comment résoudre ce genre d’équations est assez difficile.
dans cet article, nous allons apprendre comment résoudre les équations cubiques en utilisant différentes méthodes telles que la méthode de division, le théorème des facteurs et l’affacturage par regroupement.
Mais avant d’entrer dans ce sujet, discutons de ce qu’est une équation polynomiale et cubique.,
Un polynôme est une expression algébrique avec un ou plusieurs termes dans lesquels une constante et une variable sont séparés par une addition ou une soustraction signe.
La forme générale d’un polynôme est axn + bxn-1 + cxn-2 + …. + kx + l, où chaque variable a une constante qui l’accompagne comme coefficient. Les différents types de polynômes comprennent; binômes, trinômes et quadrinômes. Des exemples de polynômes sont; 3x + 1, x2 + 5XY – ax – 2AY, 6×2 + 3x + 2x + 1 etc.
une équation cubique est une équation algébrique de troisième degré.,
la forme générale d’une fonction cubique est: f (x) = ax3 + bx2 + cx1 + D. et l’équation cubique a la forme d’ax3 + bx2 + cx + d = 0, où a, b et c sont les coefficients et d est la constante.
comment résoudre les équations cubiques?
la façon traditionnelle de résoudre une équation cubique est de la réduire à une équation quadratique, puis de la résoudre soit par factorisation, soit par formule quadratique.
Comme une équation a deux racines réelles, une équation mètres pourrait avoir trois racines réelles., Mais contrairement à l’équation quadratique qui peut n’avoir aucune solution réelle, une équation cubique a au moins une racine réelle.
Les deux autres racines peuvent être réelles ou imaginaires.
chaque fois qu’on vous donne une équation cubique, ou n’importe quelle équation, vous devez toujours l’organiser d’abord sous une forme standard.
par exemple, si on vous donne quelque chose comme ça, 3×2 + x – 3 = 2/x, vous allez réorganiser dans le formulaire standard et l’écrire comme, 3×3 + x2-3x – 2 = 0. Ensuite, vous pouvez résoudre ce par toute méthode appropriée.,
nous allons voir quelques exemples ci-dessous pour mieux comprendre:
Exemple 1
Déterminer les racines de l’équation mètres 2×3 + 3×2 – 11x – 6 = 0
la Solution
Depuis le d = 6, puis les facteurs possibles sont 1, 2, 3 et 6.
appliquez maintenant le théorème des facteurs pour vérifier les valeurs possibles par essais et erreurs.
f (1) = 2 + 3 – 11 – 6 ≠ 0
f (-1) = -2 + 3 + 11 – 6 ≠ 0
f (2) = 16 + 12 – 22 – 6 = 0
par conséquent, x = 2 est la première racine.
par conséquent, les solutions sont x = 2, x = -1/2 et x = -3.,
Exemple 2
Trouver les racines de l’équation mètres x3 − 6×2 + 11x – 6 = 0
la Solution
x3 − 6×2 + 11x – 6
(x – 1) est l’un des facteurs.
En divisant x3 − 6×2 + 11x – 6 (x – 1),
⟹ (x – 1) (x2 – 5x + 6) = 0
⟹ (x – 1) (x – 2) (x – 3) = 0
Ce de l’équation mètres solutions sont x = 1, x = 2 et x = 3.
Exemple 3
Résoudre x3 – 2×2 – x + 2
la Solution
Factoriser l’équation.
x3 – 2×2 – x + 2 = x2(x – 2) – (x – 2)
= (x2 – 1) (x – 2)
= (x + 1) (x – 1) (x – 2)
x = 1, -1 et 2.,
Example 4
Solve the cubic equation x3 – 23×2 + 142x – 120
Solution
First factorize the polynomial.
x3 – 23×2 + 142x – 120 = (x – 1) (x2 – 22x + 120)
But x2 – 22x + 120 = x2 – 12x – 10x + 120
= x (x – 12) – 10(x – 12)
= (x – 12) (x – 10)
Therefore, x3 – 23×2 + 142x – 120 = (x – 1) (x – 10) (x – 12)
Equate each factor to zero.
x – 1= 0
x = 1
x – 10 = 10
x – 12= 0
x = 12
The roots of the equation are x = 1, 10 and 12.
Example 5
Solve the cubic equation x3 – 6 x2 + 11x – 6 = 0.,
Solution
pour résoudre ce problème en utilisant la méthode de division, prenez n’importe quel facteur de la constante 6;
soit x = 2
divise le polynôme par x-2 en
(x2 – 4x + 3) = 0.
Maintenant résoudre l’équation quadratique (x2 – 4x + 3) = 0, x= 1 ou x = 3
par conséquent, les solutions sont x = 2, x= 1 et x =3.
Exemple 6
Résoudre le cube de l’équation x3 – 7×2 + 4x + 12 = 0
la Solution
Laissez-f(x) = x3 – 7×2 + 4x + 12
Depuis le d = 12, les valeurs possibles sont 1, 2, 3, 4, 6 et 12.,
Par essais et erreurs, nous constatons que f (-1) = -1 – 7 – 4 + 12 = 0
Donc, (x + 1) est un facteur de la fonction.
x3 – 7×2 + 4x + 12
= (x + 1) (x2 – 8x + 12)
= (x + 1) (x – 2) (x – 6)
Donc x = -1, 2, 6
Exemple 7
Résoudre les suivantes cubique d’équation:
x3 + 3×2 + x + 3 = 0.
la Solution
x3 + 3×2 + x + 3
= (x3 + 3×2) + (x + 3)
= x2(x + 3) + 1(x + 3)
= (x + 3) (x2 + 1)
Donc, x = -1 ,1 -3.,
Example 8
Solve x3 − 6×2 + 11x − 6 = 0
Solution
Factorize
x3 − 6×2 + 11x − 6 = 0 ⟹ (x − 1) (x − 2) (x − 3) = 0
Equating each factor to zero gives;
x = 1, x = 2 and x = 3
Example 9
Solve x 3 − 4×2 − 9x + 36 = 0
Solution
Factorize each set of two terms.,ing chaque facteur à zéro, nous obtenons;
x = -3, 3 ou 4
Exemple 10
Résoudre l’équation 3×3 −16×2 + 23x − 6 = 0
la Solution
Diviser 3×3 −16×2 + 23x – 6 x -2 pour obtenir 3×2 – 1x – 9x + 3
= x (3x – 1) – 3(3x – 1)
= (x – 3) (3x – 1)
Donc, 3×3 −16×2 + 23x − 6 = (x – 2) (x – 3) (3x – 1)
Assimiler chaque facteur à zéro pour obtenir,
x = 2, 3 et 1/3
Exemple 11
Trouver les racines de 3×3 – 3×2 – 90x=0
la Solution
facteur de sortir 3x
3×3 – 3×2 – 90x ⟹3x (x2 – x – 30)
Trouver une paire de facteurs dont le produit est -30 et la somme est égale à -1.,
⟹- 6 * 5 =-30
⟹ -6 + 5 = -1
Réécrire l’équation en remplaçant le terme « bx” avec cette facteurs.
⟹ 3x
Facteur de l’équation;
⟹ 3x
= 3x (x – 6) (x + 5)
En assimilant chaque facteur à zéro, nous obtenons;
x = 0, 6, -5
Résolution des équations cubiques utilisant la méthode graphique
Si vous ne parvenez pas à résoudre l’équation mètres par aucune des méthodes ci-dessus, vous pouvez résoudre graphiquement. Pour cela, vous devez avoir une esquisse précise de l’équation cubique donnée.,
Le(s) point (S) où son graphe croise l’axe des abscisses, est une solution de l’équation. Le nombre de solutions réelles des équations cubiques est le même que le nombre de fois que son graphique croise l’axe des abscisses.
Exemple 12
Trouver les racines de x3 + 5×2 + 2x – 8 = 0 graphiquement.
Solution
dessinez simplement le graphique de la fonction suivante en substituant des valeurs aléatoires de x:
f (x) = x3 + 5×2 + 2x – 8
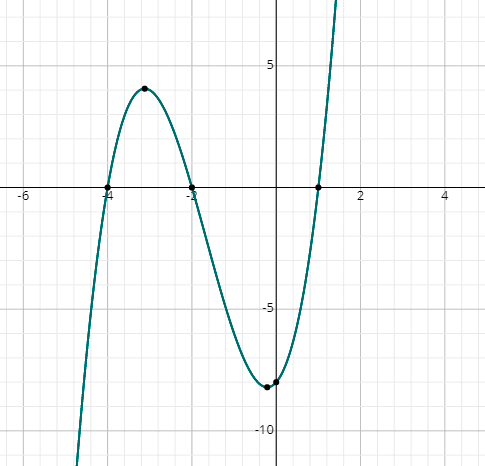
Vous pouvez voir que le graphique coupe l’axe des x en 3 points, il y a donc 3 solutions réelles.,
à Partir du graphique, les solutions sont:
x = 1, x = -2 & x = -4.
questions pratiques
résolvez les équations cubiques suivantes: