Gli algoritmi di ordinamento sono modi per organizzare una serie di elementi dal più piccolo al più grande. Questi algoritmi possono essere utilizzati per organizzare i dati disordinati e renderlo più facile da usare. Inoltre, avere una comprensione di questi algoritmi e di come funzionano è fondamentale per una forte comprensione dell’Informatica che sta diventando sempre più critica in un mondo di pacchetti premade. Questo blog si concentra sulla velocità, usi, vantaggi e svantaggi di specifici algoritmi di ordinamento.,
Sebbene esista un’ampia varietà di algoritmi di ordinamento, questo blog spiega l’inserimento diretto, l’ordinamento della shell, l’ordinamento della bolla, l’ordinamento rapido, l’ordinamento della selezione e l’ordinamento dell’heap. I primi due algoritmi (Straight Insertion e Shell Sort) ordinano gli array con l’inserimento, ovvero quando gli elementi vengono inseriti nel posto giusto. I prossimi 2 (Ordinamento a bolle e Ordinamento rapido) ordinano gli array con lo scambio che è quando gli elementi si muovono attorno all’array. L’ultimo è heap sort che ordina attraverso la selezione in cui vengono selezionati gli elementi giusti mentre l’algoritmo esegue l’array.,
Notazione Big-O
Prima che questo blog vada oltre, è essenziale spiegare i metodi che i professionisti usano per analizzare e valutare la complessità e le prestazioni dell’algoritmo. Lo standard attuale è chiamato ” Big O notation “chiamato in base alla sua notazione che è una” O “seguita da una funzione come” O(n).”
Definizione formale
Big O è usato per indicare la complessità temporale di un algoritmo o quanto spazio occupa. Questo blog si concentra principalmente sulla complessità temporale parte di questa notazione., Il modo in cui le persone possono calcolare questo è identificando il caso peggiore per l’algoritmo mirato e formulando una funzione delle sue prestazioni data una quantità n di elementi. Ad esempio, se ci fosse un algoritmo che ha cercato il numero 2 in un array, il caso peggiore sarebbe se il 2 fosse alla fine dell’array. Pertanto, la Grande notazione O sarebbe O (n) poiché dovrebbe attraversare l’intero array di elementi n prima di trovare il numero 2.
Per aiutarti, trova sotto una tabella con gli algoritmi e la sua complessità.,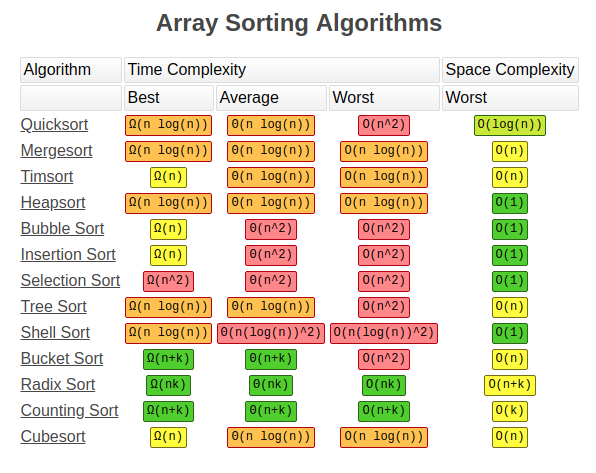
Straight Insertion Sort

Straight insertion sort è uno degli algoritmi di ordinamento più basilari che essenzialmente inserisce un elemento nella giusta posizione di una lista già ordinata. Di solito viene aggiunto alla fine di un nuovo array e si sposta verso il basso fino a trovare un elemento più piccolo grazie stesso (la posizione desiderata). Il processo si ripete per tutti gli elementi della matrice non ordinata. Considera l’array {3,1,2,5,4}, iniziamo da 3 e poiché non ci sono altri elementi nell’array ordinato, l’array ordinato diventa solo {3}., In seguito, inseriamo 1 che è più piccolo di 3, quindi si sposterebbe davanti a 3 facendo l’array {1,3}. Questo stesso processo viene ripetuto lungo la linea fino a ottenere l’array {1,2,3,4,5}.
I vantaggi di questo processo sono che è semplice e facile da implementare. Inoltre, è relativamente veloce quando ci sono piccole quantità di elementi da ordinare. Può anche trasformarsi in inserimento binario che è quando si confronta su distanze più lunghe e si restringe nel punto giusto invece di confrontare ogni singolo elemento prima del posto giusto., Tuttavia, un ordinamento di inserimento diretto è solitamente lento ogni volta che l’elenco diventa grande.
Caratteristiche Principali:
- ordinamento per Inserzione famiglia
- semplice e semplice
- caso Peggiore = O(n^2)
Python attuazione:
Shell Sort
Shell sort è un ordinamento per inserzione che prima parzialmente ordina i dati, per poi finisce l’ordinamento mediante l’esecuzione di un algoritmo di ordinamento per inserzione su tutto l’array. Generalmente inizia scegliendo piccoli sottoinsiemi dell’array e ordinando quegli array., Successivamente, ripete lo stesso processo con sottoinsiemi più grandi fino a raggiungere un punto in cui il sottoinsieme è l’array e l’intera cosa viene ordinata. Il vantaggio di farlo è che avere l’array quasi interamente ordinato aiuta l’ordinamento di inserimento finale a raggiungere o essere vicino al suo scenario più efficiente.
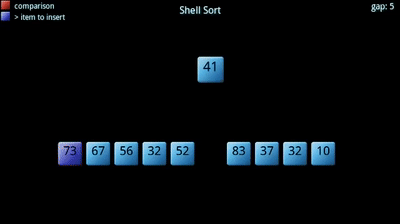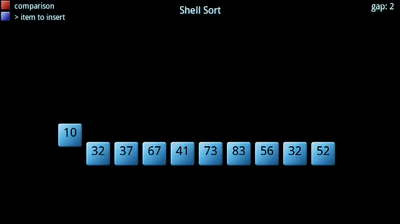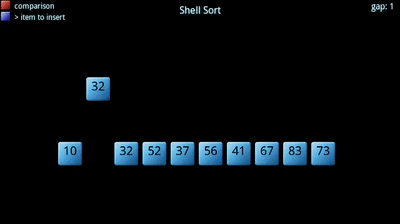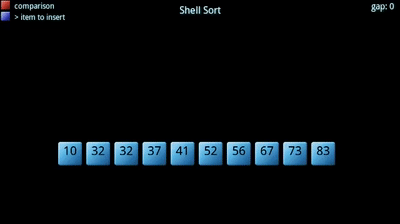
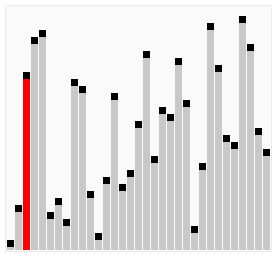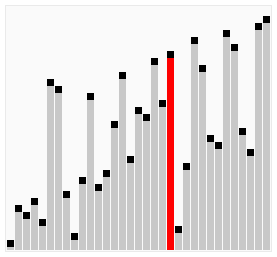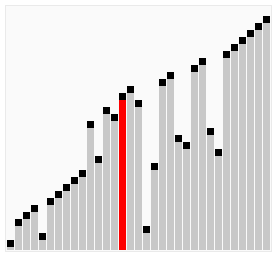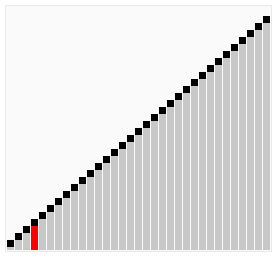
Inoltre, aumentando la dimensione dei sottoinsiemi si ottiene attraverso un termine di incremento decrescente. Il termine di incremento sceglie essenzialmente ogni elemento kth da inserire nel sottoinsieme., Inizia grande, portando a gruppi più piccoli (più sparsi) e diventa più piccolo fino a diventare 1 (tutto l’array).
Il vantaggio principale di questo algoritmo di ordinamento è che è più efficiente di un normale ordinamento di inserimento. Inoltre, esiste una varietà di algoritmi diversi che cercano di ottimizzare l’ordinamento della shell cambiando il modo in cui l’incremento diminuisce poiché l’unica restrizione è che l’ultimo termine nella sequenza di incrementi è 1. Il più popolare è di solito il metodo di Knuth che usa la formula h=((3^k)-1)/2 dandoci una sequenza di intervalli di 1 (k=1),4 (k=2),13 (k=3) e così via., D’altra parte, l’ordinamento della shell non è efficiente come altri algoritmi di ordinamento come quicksort e merge sort.
Caratteristiche Principali:
- Ordinamento per inserimento
- Grado di ottimizzare l’algoritmo cambiando incrementi
- Utilizzo di Knuth metodo, il caso peggiore è O(n^(3/2))
Python attuazione:
Bubble Sort
Bubble sort confronta adiacente elementi di un array e organizza gli elementi. Il suo nome deriva dal fatto che i grandi numeri tendono a “galleggiare” (bolla) verso l’alto., Passa attraverso un array e vede se il numero in una posizione è maggiore del numero nella posizione seguente, il che comporterebbe un aumento del numero. Questo ciclo si ripete fino a quando l’algoritmo non ha attraversato l’array senza dover modificare l’ordine. Questo metodo è vantaggioso perché è semplice e funziona molto bene per le liste per lo più ordinate. Di conseguenza, i programmatori possono implementare rapidamente e facilmente questo algoritmo di ordinamento. Tuttavia, il compromesso è che questo è uno degli algoritmi di ordinamento più lenti.,
Caratteristiche principali:Exchange sortingEasy to implementWorst Case = O(n^2)
Implementazione Python:
Quicksort
Quicksort è uno degli algoritmi di ordinamento più efficienti, e questo lo rende anche uno dei più utilizzati.La prima cosa da fare è selezionare un numero di perno, questo numero separerà i dati, alla sua sinistra ci sono i numeri più piccoli di esso e i numeri maggiori sulla destra. Con questo, abbiamo ottenuto l’intera sequenza partizionata.,Dopo che i dati sono stati partizionati, possiamo assicurare che le partizioni siano orientate, sappiamo che abbiamo valori più grandi a destra e valori più piccoli a sinistra.Il quicksort utilizza questo algoritmo divide et impera con ricorsione. Quindi, ora che abbiamo i dati divisi, usiamo la ricorsione per chiamare lo stesso metodo e passare la metà sinistra dei dati, e dopo la metà destra per continuare a separare e ordinare i dati. Alla fine dell’esecuzione, avremo i dati tutti ordinati.,
caratteristiche Principali:
- Dalla famiglia di Cambio di Ordinamento Algoritmi
- Dividere e conquistare paradigma
- Peggiore dei casi complessità O(n2)
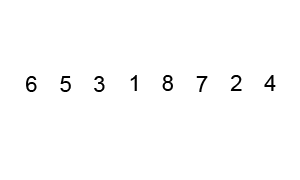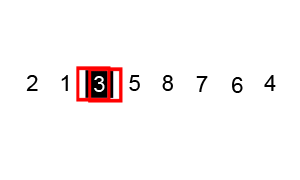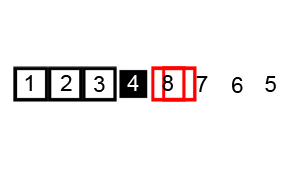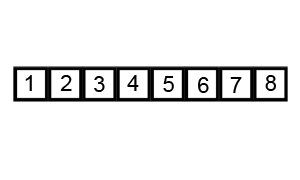
Python attuazione:
Heapsort
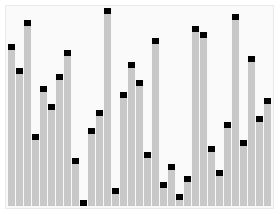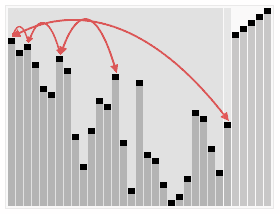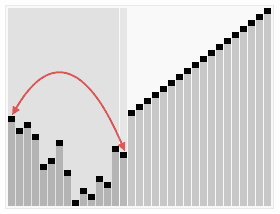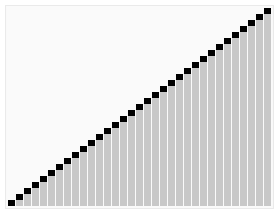
Heapsort è un algoritmo di ordinamento basato nella struttura di un heap. L’heap è una struttura dati specializzata che si trova in un albero o in un vector.In la prima fase dell’algoritmo, viene creato un albero con i valori da ordinare, a partire da sinistra, creiamo il nodo radice, con il primo valore., Ora creiamo un nodo figlio sinistro e inseriamo il valore successivo, in questo momento valutiamo se il valore impostato sul nodo figlio è più grande del valore nel nodo radice, se sì, cambiamo i valori. Facciamo questo a tutto l’albero. L’idea iniziale è che i nodi padre hanno sempre valori più grandi dei nodi figlio.
Alla fine del primo passaggio, creiamo un vettore che inizia con il valore radice e cammina da sinistra a destra riempiendo il vettore.,
Ora iniziamo a confrontare i valori dei nodi genitore e figlio cercando il valore più grande tra di loro, e quando lo troviamo, cambiamo i posti riordinando i valori. Nel primo passaggio, confrontiamo il nodo radice con l’ultima foglia dell’albero. Se il nodo radice è più grande, cambiamo i valori e continuiamo a ripetere il processo fino a quando l’ultima foglia è il valore più grande. Quando non ci sono più valori da riorganizzare, aggiungiamo l’ultima foglia al vettore e riavviamo il processo. Possiamo vedere questo nell’immagine qui sotto.,

Le caratteristiche principali dell’algoritmo sono:
- Dalla famiglia di ordinamento per selezione
- Confronti nel caso peggiore = O(n log n)
- Non stabile
Python attuazione:
Benchmark: veloce Come sono?
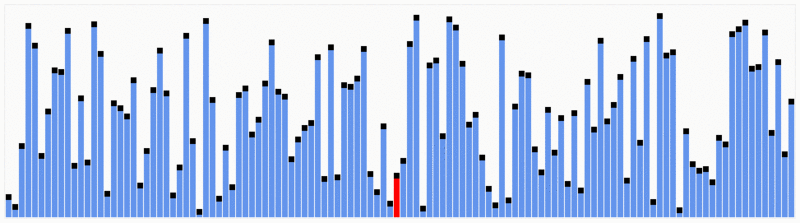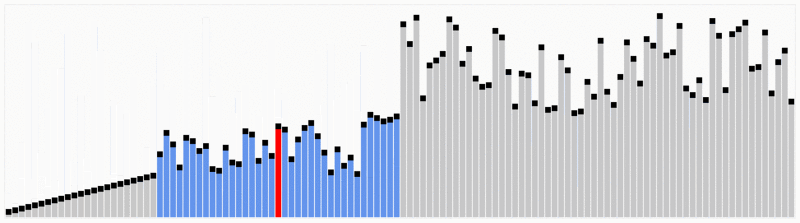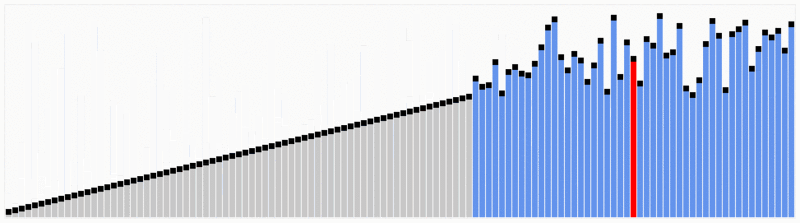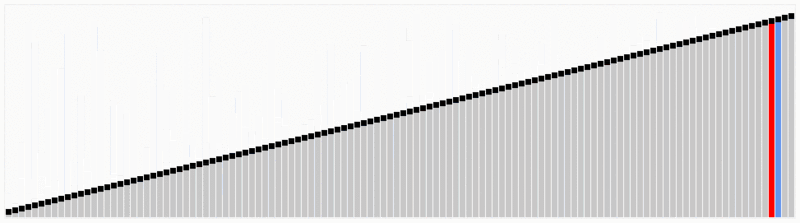
Dopo lo sviluppo degli algoritmi è bene per noi testare quanto velocemente possono essere. In questa parte abbiamo sviluppato un semplice programma usando il codice sopra per generare un benchmark di base, solo per vedere quanto tempo possono usare per ordinare un elenco di numeri interi.,Osservazioni importanti sul codice:
- Il limite di chiamata di ricorsione predefinito di Python è 1,000, in questo test stiamo usando grandi numeri, quindi avevamo bisogno di migliorare quel numero per eseguire il benchmark senza errori. Il limite è stato impostato su 10.000.
- Questo codice misura solo il tempo di esecuzione di ciascun algoritmo.
- E ‘ stato fatto 20 test con diverse dimensioni di liste che vanno da 2500 a 50000.
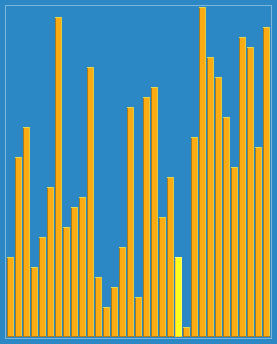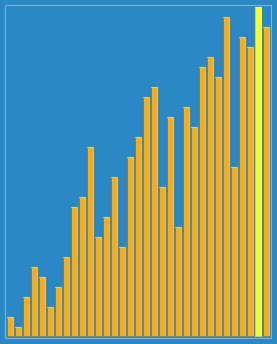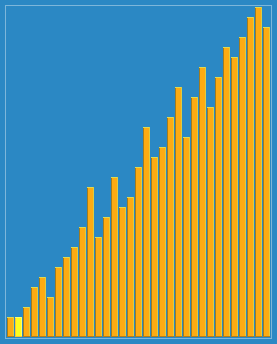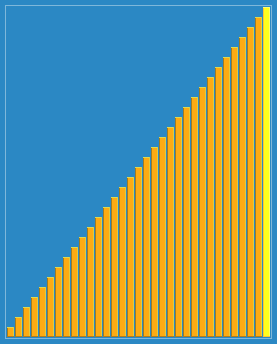
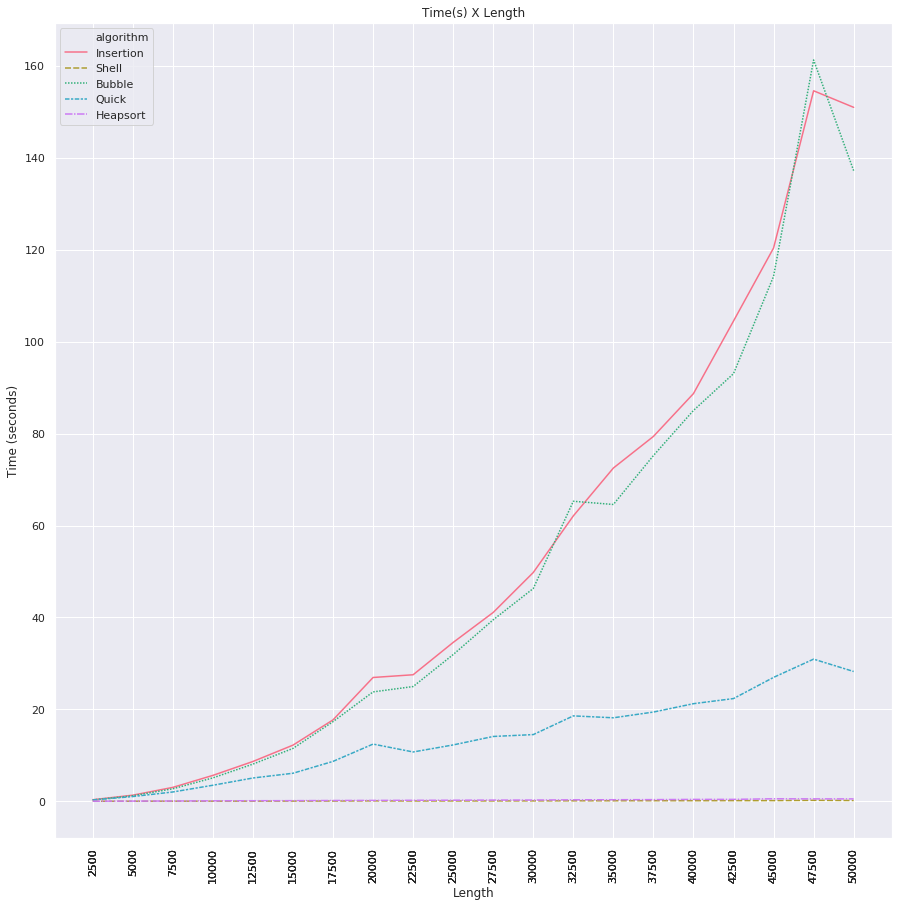
- I numeri sono stati generati randonly che vanno da 1 a 10000.,I risultati sono i seguenti:gli algoritmi di ordinamento di Shell e Heap hanno funzionato bene nonostante la lunghezza degli elenchi, nell’altro lato abbiamo scoperto che gli algoritmi di ordinamento di inserimento e ordinamento a bolle erano di gran lunga peggiori, aumentando in gran parte il tempo di calcolo. Vedere i risultati nel grafico qui sotto.
Conclusione
In questo post, abbiamo mostrato 5 degli algoritmi di ordinamento più comuni utilizzati oggi. Prima di utilizzare uno di essi è estremamente importante sapere quanto velocemente funziona e quanto spazio sta per utilizzare. Quindi è il compromesso tra complessità, velocità e volume., Un’altra caratteristica critica degli algoritmi di ordinamento che è importante conoscere è la sua stabilità. La stabilità significa che l’algoritmo mantiene l’ordine degli elementi con valori chiave uguali. Il miglior algoritmo cambia per ogni diverso insieme di dati e, di conseguenza, la comprensione dei nostri dati gioca un ruolo significativo nel processo di scelta dell’algoritmo giusto.

Come possiamo vedere, la comprensione dei nostri dati gioca un ruolo molto importante nel processo di scelta dell’algoritmo giusto.,
Se questo post ha attirato la tua attenzione, dai un’occhiata al video qui sotto, ti darà una spiegazione concisa sugli algoritmi di ordinamento 15.

Notazione O Grande – https://en.wikipedia.org/wiki/Big_O_notation
Knuth, Donald Ervin, 1938 – The art of computer programming / Donald Ervin Knuth. xiv, 782 p. 24 cm.,d=”a5b60f8536″>
Quicksort – https://commons.wikimedia.org/wiki/File:Quicksort.gif
Quicksort – http://interactivepython.org/courselib/static/pythonds/SortSearch/TheQuickSort.html
Heapsort Algorithm – https://en.wikipedia.org/wiki/Heapsort
Heapsort Algorithm – https://www.geeksforgeeks.org/heap-sort/
Bubble sort – http://interactivepython.org/runestone/static/pythonds/SortSearch/TheBubbleSort.html
Sedgewick, R.,, & Wayne, K. (2011). Algorithms, 4th Edition. (p. I–XII, 1-955). Addison-Wesley. – https://algs4.cs.princeton.edu/20sorting/
Sorting algorithms – https://brilliant.org/wiki/sorting-algorithms/