Deviazione significa solo quanto lontano dal normale
Deviazione standard
La deviazione standard è una misura di come i numeri sparsi sono.
Il suo simbolo è σ (la lettera greca sigma)
La formula è facile: è la radice quadrata della Varianza. Quindi ora chiedi: “Qual è la varianza?”
Varianza
La Varianza è definita come:
La media delle differenze quadrate rispetto alla Media.,
Per calcolare la varianza seguire questi passaggi:
- Elaborare la Media (la media semplice dei numeri)
- Quindi per ogni numero: sottrarre la Media e quadrare il risultato (la differenza al quadrato).
- Quindi calcola la media di quelle differenze al quadrato. (Perché quadrato?)
Esempio
Tu e i tuoi amici avete appena misurato le altezze dei vostri cani (in millimetri):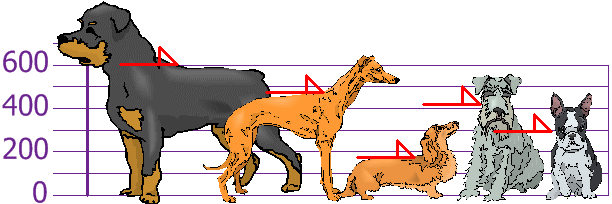
Le altezze (alle spalle) sono: 600mm, 470mm, 170mm, 430mm e 300mm.,
Find out the Mean, the Variance, and the Standard Deviation.
Your first step is to find the Mean:
Answer:
| Mean | = | 600 + 470 + 170 + 430 + 3005 |
| = | 19705 | |
| = | 394 |
so the mean (average) height is 394 mm.,2062 + 762 + (−224)2 + 362 + (−94)25
So the Variance is 21,704
And the Standard Deviation is just the square root of Variance, so:
| Standard Deviation | ||
| σ | = | √21704 |
| = | 147.,32… | |
| = | 147 (al mm più vicino) | |
E la cosa buona della Deviazione Standard è che è utile. Ora possiamo mostrare quali altezze sono all’interno di una Deviazione standard (147mm) della Media: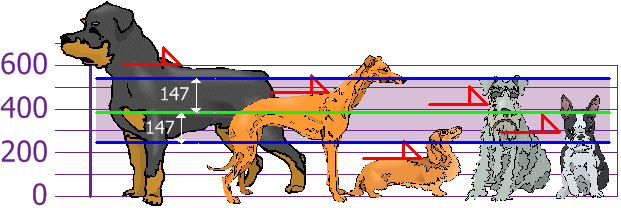
Quindi, usando la Deviazione standard abbiamo un modo “standard” di sapere cosa è normale e cosa è extra large o extra small.
I rottweiler sono cani alti. E i bassotti sono un po ‘ corti, giusto?,
Usando
Possiamo aspettarci che circa il 68% dei valori sia all’interno della deviazione standard plus-or-minus1.
Leggi la distribuzione normale standard per saperne di più.
Prova anche il calcolatore della deviazione standard.
Ma … c’è un piccolo cambiamento con i dati di esempio
Il nostro esempio è stato per una popolazione (i 5 cani sono gli unici cani a cui siamo interessati).
Ma se i dati sono un campione (una selezione presa da una popolazione più grande), il calcolo cambia!,
Quando hai “N” valori di dati che sono:
- La popolazione: dividi per N quando calcoliamo la varianza (come abbiamo fatto noi)
- Un esempio: dividi per N-1 quando calcoliamo la varianza
Tutti gli altri calcoli rimangono gli stessi, incluso il modo in cui abbiamo calcolato la media.,
Esempio: se il nostro 5 cani sono solo un esempio di un maggiore popolazione di cani, dividere per 4 invece di 5 come questo:
Pensate a come una “correzione”, quando i dati è solo un esempio.,
Formule
Qui ci sono due formule, ha spiegato la Deviazione Standard Formule se volete saperne di più:
|
La “Deviazione Standard della Popolazione”: |
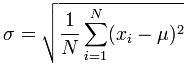 |
|
| La “Deviazione Standard”: | 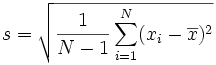 |
Sembra complicato, ma l’importante è a
dividere per N-1 (anziché N) calcolo della Varianza campionaria.
