Funzione di distribuzione di Poisson

La distribuzione di Poisson fornisce un modo utile per valutare la percentuale di tempo in cui ci si aspetta un determinato intervallo di risultati. Si potrebbe desiderare di proiettare un limite superiore ragionevole su qualche evento dopo aver effettuato una serie di osservazioni.,

Ad esempio, se hai misurato un certo tipo di evento speciale solo una volta (x=1) durante la tua corsa su un grande acceleratore dopo aver osservato n eventi, allora potresti voler proiettare quanti eventi dovresti osservare per avere un livello di confidenza del 90% di vedere almeno un ulteriore evento speciale di questo tipo. (Questo aiuterebbe a difendere la tua richiesta per più tempo sull’acceleratore la prossima volta!) Questo tipo di proiezione è adatto alle statistiche di Poisson., Un approccio conveniente al calcolo consiste nel calcolare il valore medio “a” dell’osservazione per la quale l’osservazione del valore x=0 è probabile del 10%. In termini di distribuzione di Poisson, questa condizione può essere espressa come

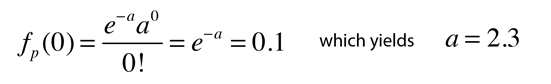
Ora, dal momento che la media è a = n p e la probabilità p=1/n, dove n è il numero delle tue precedenti osservazioni, ne consegue che per ottenere un 90% livello di confidenza di vedere un altro evento speciale, si dovrebbe osservare n’ = 2.3 n più eventi. Cioè, devi osservare 2.,3 volte tanto quanto hai fatto la prima volta per essere sicuro al 90% di vederne un altro.

Un altro modo di interpretare questo risultato è che se osservi n eventi senza vedere nessuno degli eventi speciali desiderati, allora con il 90% di sicurezza puoi dire che il valore medio per l’osservazione di tali eventi è inferiore a 2.3 = a dove a=np è il valore medio standard. Sulla base di un piccolo numero di osservazioni di eventi che si presume agiscano per pura probabilità, è possibile effettuare una proiezione del limite superiore per tali eventi a un livello scelto di fiducia.,