Introduction to Survival Analysis: the Kaplan-Meier estimator (Italiano)

Nel mio precedente articolo, ho descritto i potenziali casi d’uso dell’analisi di sopravvivenza e introdotto tutti gli elementi costitutivi necessari per comprendere le tecniche utilizzate per analizzare i dati time-to-event.

Continuo la serie spiegando forse l’approccio più semplice, ma molto perspicace all’analisi della sopravvivenza: lo stimatore Kaplan — Meier. Dopo un’introduzione teorica, vi mostrerò come effettuare l’analisi in Python utilizzando la popolare librerialifetimes.,

Lo stimatore Kaplan-Meier (noto anche come stimatore del limite di prodotto, vedrai perché più avanti) è una tecnica non parametrica di stimare e tracciare la probabilità di sopravvivenza in funzione del tempo. Spesso è il primo passo per effettuare l’analisi di sopravvivenza, in quanto è l’approccio più semplice e richiede il minimo presupposto. Per eseguire l’analisi utilizzando l’approccio Kaplan-Meier, assumiamo quanto segue:

• L’evento di interesse è inequivocabile e avviene in un momento chiaramente specificato.,
• La probabilità di sopravvivenza di tutte le osservazioni è la stessa, non importa esattamente quando sono entrate nello studio.
• Le osservazioni censurate hanno le stesse prospettive di sopravvivenza delle osservazioni che continuano ad essere seguite.

Nei casi reali, non conosciamo mai la vera funzione di sopravvivenza. Ecco perché con lo stimatore Kaplan-Meier, approssimiamo la vera funzione di sopravvivenza dai dati raccolti.,tor è definito come la frazione di osservazioni che sono sopravvissuti per un certo periodo di tempo e con le stesse condizioni ed è dato dalla seguente formula:

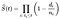
in cui:

• t_i è un momento in cui almeno un evento di successo,
• d_i è il numero di eventi che è accaduto al momento t_i,
• n_i rappresenta il numero di individui noti per essere sopravvissuto fino al momento in cui t_i (coloro che non hanno ancora avuto l’evento morte o sono state censurate)., O per dirla in modo diverso, il numero di osservazioni a rischio al momento t_i.

Dal simbolo del prodotto nella formula, possiamo vedere la connessione con l’altro nome del metodo, lo stimatore del limite di prodotto. La probabilità di sopravvivenza al tempo t è uguale al prodotto della percentuale di probabilità di sopravvivere al tempo t e ogni tempo precedente.

Ciò che più spesso associamo a questo approccio all’analisi di sopravvivenza e ciò che generalmente vediamo nella pratica sono le curve di Kaplan-Meier — una trama dello stimatore di Kaplan-Meier nel tempo., Possiamo usare quelle curve come strumento esplorativo-per confrontare la funzione di sopravvivenza tra coorti, gruppi che hanno ricevuto qualche tipo di trattamento o meno, gruppi comportamentali, ecc.

La linea di sopravvivenza è in realtà una serie di passi orizzontali decrescenti, che si avvicinano alla forma della vera funzione di sopravvivenza della popolazione data una dimensione del campione abbastanza grande., In pratica, la trama è spesso accompagnata da intervalli di confidenza, per mostrare quanto siamo incerti sulle stime puntuali — ampi intervalli di confidenza indicano un’elevata incertezza, probabilmente dovuta allo studio che contiene solo pochi partecipanti — causato da entrambe le osservazioni che muoiono e vengono censurate. Per maggiori dettagli sul calcolo degli intervalli di confidenza utilizzando il metodo Greenwood, vedere .,

L’interpretazione della curva di sopravvivenza è abbastanza semplice, l’asse y rappresenta la probabilità che il soggetto non ha ancora sperimentato l’evento di interesse, dopo essere sopravvissuto fino al tempo t, rappresentato sull’asse x. Ogni calo della funzione di sopravvivenza (approssimata dallo stimatore Kaplan-Meier) è causato dall’evento di interesse che si verifica per almeno un’osservazione.,

La lunghezza effettiva della linea verticale rappresenta la frazione di osservazioni a rischio che hanno sperimentato l’evento al tempo t. Ciò significa che una singola osservazione (non in realtà la stessa, ma semplicemente singolare) che sperimenta l’evento in due momenti diversi può comportare una diminuzione della dimensione della differenza — a seconda del numero di osservazioni a rischio. In questo modo, l’altezza della goccia può anche informarci sul numero di osservazioni a rischio (anche quando non dichiarato e/o non ci sono intervalli di confidenza).,

Quando nessuna osservazione ha sperimentato l’evento di interesse o alcune osservazioni sono state censurate, non vi è alcun calo nella curva di sopravvivenza.

Il log-rank test

Abbiamo imparato a utilizzare il metodo di Kaplan-Meier stimatore per approssimare la vera funzione di sopravvivenza di una popolazione., E sappiamo che possiamo tracciare più curve per confrontare le loro forme, ad esempio, dal sistema operativo utilizzato dagli utenti della nostra app mobile. Tuttavia, non abbiamo ancora uno strumento che consenta effettivamente il confronto. Beh, almeno uno più rigoroso di eyeballing le curve.

Questo è quando il test log-rank entra in gioco. È un test statistico che confronta le probabilità di sopravvivenza tra due gruppi (o più, per questo si veda l’implementazione Python). L’ipotesi nulla del test afferma che non vi è alcuna differenza tra le funzioni di sopravvivenza dei gruppi considerati.,

Il test log-rank utilizza le stesse ipotesi dello stimatore Kaplan-Meier. Inoltre, esiste l’ipotesi di pericoli proporzionali: il rapporto di pericolo (vedere l’articolo precedente per un promemoria sul tasso di pericolo) dovrebbe essere costante per tutto il periodo di studio. In pratica, ciò significa che il test log-rank potrebbe non essere un test appropriato se le curve di sopravvivenza si incrociano. Tuttavia, questo è ancora un argomento di dibattito attivo, si prega di vedere e .

Per brevità, non copriamo la matematica dietro il test. Se siete interessati, si prega di consultare questo articolo o .,

Errori comuni con Kaplan-Meier

In questa parte, ho voluto menzionare alcuni degli errori comuni che possono verificarsi mentre si lavora con lo stimatore Kaplan-Meier.

Rimozione dei dati censurati

Si potrebbe essere tentati di rimuovere i dati censurati in quanto può alterare significativamente la forma della curva Kaplan-Meier, tuttavia, questo può portare a gravi pregiudizi, quindi dovremmo sempre includerlo durante il montaggio del modello.,

Interpretando le estremità delle curve

Prestare particolare attenzione quando si interpreta il termine delle curve di sopravvivenza, come tutte le grandi gocce di chiudere per la fine dello studio, può essere spiegato solo da un paio di osservazioni di arrivare a questo punto di tempo (questo dovrebbe anche essere indicato da più ampi intervalli di confidenza)

Dichotomizing variabili continue

Da dichotomizing I media utilizzando la mediana o “ottimale” cut-off point per la creazione di gruppi come “low” e “high” per quanto riguarda eventuali continuo metrica., Questo approccio può creare molteplici problemi:

• Trovare un punto di cut-off “ottimale” può essere molto dipendente dal set di dati e impossibile da replicare in diversi studi. Inoltre, facendo confronti multipli, rischiamo di aumentare le possibilità di falsi positivi (trovando una differenza nelle funzioni di sopravvivenza, quando in realtà non ce n’è).
• La dicotomizzazione diminuisce la potenza del test statistico forzando tutte le misurazioni a un valore binario, che a sua volta può portare alla necessità di una dimensione del campione molto più grande richiesta per rilevare un effetto., Vale anche la pena ricordare che con l’analisi di sopravvivenza, la dimensione del campione richiesta si riferisce al numero di osservazioni con l’evento di interesse.
• Quando dicotomizziamo, facciamo scarse ipotesi sulla distribuzione del rischio tra le osservazioni. Supponiamo di utilizzare l’età di 50 come divisione tra pazienti giovani e anziani. Se lo facciamo, assumiamo che un 18enne sia nello stesso gruppo di rischio di un 49enne, il che non è vero nella maggior parte dei casi.,

Contabilizzazione di un solo predittore

Lo stimatore Kaplan-Meier è un metodo univariabile, in quanto approssima la funzione di sopravvivenza usando al massimo una variabile / predittore. Di conseguenza, i risultati possono essere facilmente distorti, esagerando o perdendo il segnale. Ciò è causato dal cosiddetto bias variabile omessa, che fa sì che l’analisi assuma che i potenziali effetti di più predittori dovrebbero essere attribuiti solo a quello singolo, che prendiamo in considerazione. Per questo motivo, dovrebbero essere usati invece metodi multivariabili come la regressione di Cox.,

Esempio in Python

È tempo di implementare ciò che abbiamo imparato nella pratica. Iniziamo importando tutte le librerie richieste.

Quindi, carichiamo il set di dati e facciamo alcune piccole dispute per farlo funzionare bene con la libreria lifelines. Per l’analisi, utilizziamo il popolare set di dati di Churn dei clienti Telco (disponibile qui o sul mio GitHub)., Il set di dati contiene informazioni client di un telefono / internet provider, compreso il loro mandato, che tipo di servizi che utilizzano, alcuni dati demografici, e, infine, il flag che indica churn.,

Per questa analisi, abbiamo utilizzato i seguenti colonne:

• tenure — il numero di mesi il cliente è rimasto con l’azienda,
• churn — se il cliente ha sbattuto (codificato in binario: 1 se l’evento è accaduto, 0 altrimenti),
• PaymentMethod:— che tipo di metodo di pagamento clienti abituati.,

Per lo scenario di base, in realtà abbiamo solo bisogno del time-to-event e del flag che indica se l’evento di interesse si è verificato.

KaplanMeierFitter funziona allo stesso modo per le classi conosciuto da scikit-learn: dobbiamo prima creare un’istanza di un oggetto della classe e quindi utilizzare il fit metodo per adattare il modello ai dati., Durante la stampa, specifichiamo at_risk_counts=True per visualizzare inoltre informazioni sul numero di osservazioni a rischio in determinati punti del tempo.

Normalmente, saremmo interessati a il tempo mediano di sopravvivenza, che è il momento in cui, in media, il 50% della popolazione è già morto, o in questo caso, agitato., Possiamo accedervi usando la seguente riga:

kmf.median_survival_time_

Tuttavia, in questo caso, il comando restituisceinf, come possiamo vedere dalla curva di sopravvivenza che in realtà non osserviamo quel punto nei nostri dati.

Abbiamo visto il caso d’uso di base, ora complichiamo l’analisi e tracciamo le curve di sopravvivenza per ogni variante del metodo di pagamento., Possiamo farlo utilizzando il seguente codice:

Esecuzione del blocco di codice genera il seguente trama:

Possiamo vedere che la probabilità di sopravvivenza è sicuramente il più basso per il controllo elettronico, mentre le curve di bonifico bancario/carta di credito sono molto simili., Questo è un momento perfetto per utilizzare il test log-rank per vedere se sono effettivamente diversi.

La seguente tabella presenta i risultati.

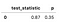
guardando il p-valore di 0,35, siamo in grado di vedere che non ci sono motivi per rifiutare l’ipotesi affermando che la sopravvivenza funzioni sono identiche. Per questo esempio, abbiamo confrontato solo due metodi di pagamento., Tuttavia, ci sono sicuramente più combinazioni che potremmo testare. C’è una comoda funzione chiamata pairwise_logrank_test, che rende il confronto molto semplice.

Nella tabella, si veda il precedente confronto che abbiamo fatto, così come tutte le altre combinazioni. Il bonifico bancario vs., la carta di credito è l’unico caso in cui non dovremmo rifiutare l’ipotesi nulla. Inoltre, dovremmo essere cauti nell’interpretare i risultati del test log-rank, come possiamo vedere nella trama sopra che le curve per il bonifico bancario e i pagamenti con carta di credito si incrociano effettivamente, quindi l’assunzione di rischi proporzionali viene violata.

Ci sono altre due cose che possiamo facilmente testare usando la libreria lifelines. Il primo è il test di log-rank multivariato, in cui l’ipotesi nulla afferma che tutti i gruppi hanno lo stesso processo di generazione della “morte”, quindi le loro curve di sopravvivenza sono identiche.,

I risultati del test indicano che dobbiamo rifiutare l’ipotesi nulla, in modo che le curve di sopravvivenza non sono identici, di cui abbiamo già visto nella trama.

Infine, possiamo testare la differenza di sopravvivenza in un punto specifico nel tempo. Tornando all’esempio, nella trama, possiamo vedere che le curve sono più distanti intorno a t = 60., Vediamo se questa differenza è statisticamente significativa.

guardando il test p-value, non vi è alcun motivo per rifiutare l’ipotesi affermando che non vi è alcuna differenza tra la sopravvivenza a quel punto del tempo.

Conclusioni

In questo articolo, ho descritto uno strumento molto popolare per condurre l’analisi di sopravvivenza: lo stimatore Kaplan — Meier., Abbiamo anche coperto il test log-rank per confrontare due / più funzioni di sopravvivenza. L’approccio descritto è molto popolare, tuttavia, non senza difetti. Prima di concludere, diamo un’occhiata ai pro e ai contro dello stimatore/curve di Kaplan-Meier.

Vantaggi:

• Fornisce la visione media della popolazione, anche per gruppi.
• Non richiede molte funzionalità — solo le informazioni sul time-to-event e se l’evento si è effettivamente verificato. Inoltre, possiamo utilizzare tutte le caratteristiche categoriali che descrivono i gruppi.,
• Gestisce automaticamente lo squilibrio di classe, poiché praticamente qualsiasi proporzione tra morte e eventi censurati è accettabile.
• Poiché si tratta di un metodo non parametrico, vengono fatte poche ipotesi sulla distribuzione sottostante dei dati.

Svantaggi:

• Non possiamo valutare l’entità dell’impatto del predittore sulla probabilità di sopravvivenza.
• Non possiamo contemporaneamente tenere conto di più fattori per le osservazioni, ad esempio, il paese di origine e il sistema operativo del telefono.,
• L’assunzione di indipendenza tra censura e sopravvivenza (al tempo t, le osservazioni censurate dovrebbero avere la stessa prognosi di quelle senza censura) può essere inapplicabile/irrealistica.
• Quando la distribuzione dei dati sottostante è (in una certa misura) nota, l’approccio non è accurato come alcune tecniche concorrenti.

Riassumendo, anche con alcuni svantaggi le curve di sopravvivenza Kaplan-Meier sono un ottimo punto di partenza durante lo svolgimento di analisi di sopravvivenza., Nel farlo, possiamo ottenere preziose informazioni sui potenziali predittori della sopravvivenza e accelerare i nostri progressi con alcune tecniche più avanzate (che descriverò nei prossimi articoli).

Puoi trovare il codice usato per questo articolo sul mio GitHub. Come sempre, qualsiasi feedback costruttivo è benvenuto. Puoi contattarmi su Twitter o nei commenti.

Nel caso in cui hai trovato questo articolo interessante, potrebbero piacerti anche gli altri della serie:

S. Sawyer (2003)., Gli intervalli di confidenza di Greenwood ed esponenziali di Greenwood nell’analisi di sopravvivenza-disponibili qui

Curve di sopravvivenza di Kaplan-Meier e test di Log-Rank-disponibili qui

Pericoli non proporzionali-e allora? – disponibile qui

Bouliotis, G., & Billingham, L. (2011). Crossing survival curves: alternative al test log-rank. Prove, 12 (S1), A137.