Les chiffres indiens discutés dans notre article Les chiffres indiens forment la base des systèmes numériques Européens qui sont maintenant largement utilisés. Cependant, ils n’ont pas été transmis directement de L’Inde à L’Europe, mais sont plutôt venus en premier aux peuples arabes/islamiques et d’eux à L’Europe. L’histoire de cette transmission n’est cependant pas simple. Les parties orientale et occidentale du monde arabe ont toutes deux vu des développements distincts des chiffres indiens avec relativement peu d’interaction entre les deux., Par la partie occidentale du monde arabe, nous entendons les régions comprenant principalement L’Afrique du Nord et L’Espagne. La Transmission vers l’Europe s’est faite par cette route arabe occidentale, entrant d’abord en Europe par L’Espagne.
Il y a d’autres complications dans l’histoire, cependant, car ce n’était pas simplement que les Arabes ont repris le système de numéro Indien. Des systèmes de numérotation assez différents ont été utilisés simultanément dans le monde arabe sur une longue période., Par exemple, il y avait au moins trois types différents d’arithmétique utilisés dans les pays arabes au XIe siècle: un système dérivé de compter sur les doigts avec les chiffres écrits entièrement en mots, cette arithmétique de calcul des doigts était le système utilisé par le monde des affaires; le système sexagésimal avec des chiffres désignés par des lettres de l’alphabet arabe; et l’arithmétique des chiffres et des fractions indiennes avec le système décimal-valeur.
le premier signe que les chiffres indiens se déplaçaient vers l’Ouest provient d’une source antérieure à la montée des nations arabes., En 662 après JC Severus Sebokht, un évêque nestorien qui vivait à Keneshra sur L’Euphrate, a écrit:-
j’omettrai toute discussion sur la science des Indiens, … , de leurs découvertes subtiles en astronomie, découvertes plus ingénieuses que celles des Grecs et des Babyloniens, et de leurs précieuses méthodes de calcul qui dépassent la description. Je voudrais seulement dire que ce calcul se fait au moyen de neuf signes., Si ceux qui croient, parce qu’ils parlent Grec, qu’ils sont arrivés aux limites de la science, liraient les textes indiens, ils seraient convaincus, même si un peu tard dans la journée, qu’il y en a d’autres qui savent quelque chose de valeur.
ce passage indique clairement que la connaissance du système de numérotation Indien était connue dans les pays qui allaient bientôt faire partie du monde arabe dès le VIIe siècle. Le passage lui-même, bien sûr, suggérerait certainement que peu de gens dans cette partie du monde connaissaient quoi que ce soit du système., Severus Sebokht en tant qu’évêque chrétien aurait été intéressé par le calcul de la date de Pâques (un problème pour les églises chrétiennes depuis plusieurs centaines d’années). Cela l’a peut-être encouragé à découvrir les travaux d’astronomie des Indiens et, bien sûr, il y trouverait l’arithmétique des neuf symboles.
En 776 après JC, l’empire arabe commençait à prendre forme et nous avons une autre référence à la transmission des chiffres indiens., Nous citons un ouvrage D’Al-Qifti Chronologie des savants écrit vers la fin du 12ème siècle mais citant des sources beaucoup plus anciennes: –
… une personne de L’Inde s’est présentée devant le calife al-Mansur dans l’année qui connaissait bien la méthode de calcul siddhanta liée au mouvement des corps célestes, et ayant des moyens de calculer des équations basées sur la demi-corde calculée en demi-degrés … Tout cela est contenu dans une œuvre … d’où il prétendait avoir pris le demi-accord calculé pendant une minute., Al-Mansur a ordonné que ce livre soit traduit en arabe, et un travail à écrire, basé sur la traduction, pour donner aux Arabes une base solide pour calculer les mouvements des planètes …
maintenant dans (où une citation plus longue est donnée) Ifrah essaie de déterminer à quel travail indien est fait référence. Il conclut que L’œuvre était très probablement le Brahmasphutasiddhanta de Brahmagupta (L’ouverture de l’univers) qui a été écrit en 628., Peu importe si Ifrah a raison, puisque tous les textes indiens après L’Aryabhatiya d’Aryabhata I utilisaient le système de numérotation indien des neuf signes, certainement à partir de cette époque, les Arabes avaient une traduction en arabe d’un texte écrit dans le système de numérotation Indien.
On prétend souvent que le premier texte arabe écrit pour expliquer le système de numération indienne a été écrit par al-Khwarizmi. Cependant, il y a des difficultés ici que de nombreux auteurs ont tendance à ignorer., Le texte arabe est perdu mais une traduction latine du XIIe siècle, Algoritmi de numero Indorum gave a donné naissance au mot algorithme dérivant de son nom dans le titre. Malheureusement, la traduction latine est connue pour être beaucoup modifiée par rapport au texte original d’al-Khwarizmi (dont même le titre est inconnu). Le texte Latin décrit certainement le système de valeur de lieu indien des chiffres basés sur 1, 2, 3, 4, 5, 6, 7, 8, 9, et 0. La première utilisation du zéro comme support de place dans la notation de base positionnelle est considérée par certains comme due à al-Khwarizmi dans ce travail., La difficulté qui se pose est qu’al-Baghdadi se réfère à l’original arabe qui, contrairement à ce que l’on pensait à l’origine, ne semble pas être un travail sur les chiffres indiens mais plutôt un travail sur les méthodes de comptage des doigts. Cela ressort clairement des références d’al-Baghdadi à l’œuvre perdue. Cependant, les nombreuses références au livre d’al-Khwarizmi sur les neuf symboles Indiens doivent signifier qu’il a écrit un tel ouvrage. Un certain degré de mystère demeure.
Au début, les méthodes indiennes ont été utilisées par les arabes avec un panneau de poussière., En fait, dans la partie occidentale du monde arabe, les chiffres indiens sont devenus connus sous le nom de chiffres Guba (ou Gubar ou Ghubar) du mot arabe signifiant « poussière ». Un panneau de poussière a été utilisé parce que les méthodes arithmétiques nécessitaient le déplacement des nombres dans le calcul et le frottement de certains d’entre eux au fur et à mesure du calcul. Le panneau de poussière a permis cela de la même manière que l’on peut utiliser un tableau noir, de la craie et une gomme à effacer., Tout étudiant qui a assisté à des conférences où le conférencier change et remplace continuellement des parties des mathématiques au fur et à mesure que la démonstration progresse comprendra l’inconvénient du tableau de poussière!
vers le milieu du Xe siècle al-Uqlidisi a écrit Kitab al-fusul fi al-hisab al-Hindi which qui est le premier livre survivant qui présente le système Indien., Al-Uqlidisi y soutient que le système a une valeur pratique:-
la plupart des arithméticiens sont obligés de l’utiliser dans leur travail: car il est facile et immédiat, nécessite peu de mémorisation, fournit des réponses rapides, demande peu de réflexion … Par conséquent, nous disons que c’est une science et une pratique qui nécessite un outil, tel qu’un écrivain, un artisan, un chevalier a besoin de mener leurs affaires; puisque si l’artisan a du mal à trouver ce dont il a besoin pour son métier, il ne réussira jamais; pour le saisir il n’y a pas de difficulté, d’impossibilité ou,
dans la quatrième partie de ce livre, al-Uqlidisi a montré comment modifier les méthodes de calcul avec des symboles Indiens, qui avaient nécessité un panneau de poussière, à des méthodes qui pouvaient être effectuées avec un stylo et du papier. Certes, le fait que le système Indien exige un panneau de poussière a été l’un des principaux obstacles à son acceptation., Par exemple As-Suli, après avoir loué le système indien pour sa grande simplicité, a écrit dans la première moitié du Xe siècle:-
les scribes officiels évitent néanmoins de l’utiliser car il nécessite du matériel et ils considèrent qu’un système qui ne nécessite que les membres du corps est plus sûr et plus
le travail D’Al-Uqlidisi est donc important pour tenter de lever l’un des obstacles à l’acceptation des neuf symboles Indiens., Il est également historiquement important car c’est le premier texte connu offrant un traitement direct des fractions décimales.
bien que de nombreux chercheurs trouvent le calcul avec des symboles Indiens utiles dans leur travail, la communauté des affaires a continué à utiliser leur arithmétique des doigts tout au long du dixième siècle. Abu’l-Wafa, qui était lui-même un expert dans l’utilisation des chiffres indiens, a néanmoins écrit un texte sur la façon d’utiliser l’arithmétique du calcul au doigt car c’était le système utilisé par la communauté des affaires et le matériel pédagogique destiné à ces personnes devait être écrit en utilisant le système approprié., Donnons un peu d’informations sur les chiffres des lettres arabes qui sont contenus dans le travail D’Abu’l-Wafa.
Les chiffres étaient représentés par des lettres mais pas dans l’ordre du dictionnaire. Le système était connu comme huruf al jumal qui signifiait « lettres pour calculer » et aussi parfois comme abjad qui n’est que les quatre premiers nombres (1 = a, 2 = b, j = 3, d = 4). Les chiffres de 1 à 9 étaient représentés par des lettres, puis les chiffres 10, 20, 30,…, 90 par les neuf lettres (10 = o, 20 = k, 30 = l, 40 = m, …), puis 100, 200, 300, … , 900 par les lettres suivantes (100 = q, 200 = r, 300 = sh, 400 = ta, …,). Il y avait 28 lettres arabes et il en restait donc une qui a été utilisée pour représenter 1000.
Les astronomes arabes ont utilisé une version base 60 du système de lettres arabes. Bien que l’arabe soit écrit de droite à gauche, nous donnerons un exemple d’écriture dans le style de gauche à droite que nous utilisons pour écrire l’anglais. Un nombre, disons 43° 21 ’14 », aurait été écrit comme » mj ka yd « dans cette version de base 60 des lettres » abjad » pour le calcul.
Un contemporain d’al-Baghdadi, écrivant vers le début du XIe siècle, était ibn Sina (plus connu en Occident sous le nom D’Avicenne)., Nous connaissons de nombreux détails de sa vie car il a écrit une autobiographie. Certes, ibn Sina était un enfant remarquable, avec une mémoire et une capacité d’apprendre qui ont étonné les érudits qui se sont rencontrés dans la maison de son père. Un groupe d’érudits D’Egypte est venu à la maison de son père vers 997 quand ibn Sina avait dix ans et ils lui ont enseigné l’arithmétique indienne. Il raconte également avoir appris le calcul et l’algèbre Indiens par un vendeur de légumes., Tout cela montre qu’au début du XIe siècle, le calcul avec les symboles Indiens était assez répandu et, de manière significative, était connu d’un marchand de légumes.
Qu’en est-il des chiffres eux-mêmes. Nous avons vu dans l’article chiffres indiens que la forme des chiffres eux-mêmes variait selon les régions et changeait au fil du temps. Exactement la même chose s’est produite dans le monde arabe.
Voici un exemple d’une forme précoce de chiffres Indiens utilisés dans la partie orientale de l’empire arabe., Il provient d’un travail d’al-Sijzi, pas un travail original de lui, mais plutôt le travail d’un autre mathématicien qui Al-sijzi copié à Shiraz et daté sa copie 969.
Les chiffres du traité d’al-Sizji de 969
Les chiffres avaient quelque peu changé de forme 100 ans plus tard lorsque cette copie d’un des textes astronomiques d’al-Biruni a été faite. Voici les chiffres tels qu’ils apparaissent dans un 1082 copie.,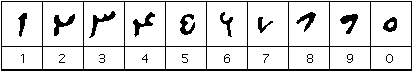
Les chiffres du traité d’Al-Biruni copié en 1082
En fait, un examen plus approfondi montrera qu’entre 969 et 1082, le plus grand changement dans les chiffres était le fait que le 2 et le 3 ont été tournés de 90°. Il y a une raison à ce changement qui s’est produit en raison de la façon dont les scribes écrivaient, car ils écrivaient sur un rouleau qu’ils enroulaient de droite à gauche sur leur corps alors qu’ils étaient assis les jambes croisées. Les scribes donc, au lieu d’écrire de droite à gauche (la manière standard que l’arabe était écrit) ont écrit en lignes de haut en bas., Le script a été pivoté lorsque le défilement a été lu et les caractères lorsqu’ils étaient alors dans la bonne orientation.
voici un exemple de la façon dont le texte a été écrit
peut-être parce que les scribes n’avaient pas beaucoup d’expérience dans l’écriture des chiffres indiens, ils ont écrit 2 et 3 dans le bon sens au lieu de les écrire pivotés de 90° afin,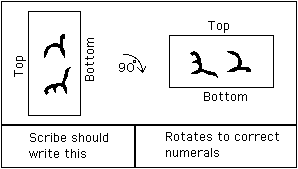
voici un exemple de ce que le scribe devrait écrire
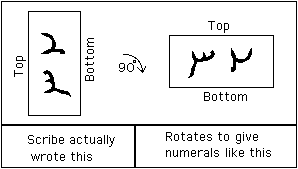
Et voici ce que le scribe a réellement écrit
la forme des chiffres dans l’ouest de l’empire arabe semble plus familière à ceux qui utilisent les chiffres européens puisque c’est à partir de ces chiffres que le système de numération Indien atteint l’Europe.,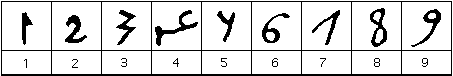
la forme des chiffres d’al-Banna Al-Marrakushi
Il a donné cette forme des chiffres dans son livre d’arithmétique pratique écrit vers le début du XIVe siècle. Il a vécu la majeure partie de sa vie au Maroc qui était en contact étroit avec al-Andalus, ou Andalousie, qui était la région contrôlée par les Arabes dans le sud de l’Espagne.
Le premier exemple survivant des chiffres indiens dans un document en Europe était, cependant, bien avant l’époque d’al-Banna. Les chiffres apparaissent dans le Codex Vigilanus copié par un moine en Espagne en 976., Cependant, la majeure partie de l’Europe n’était pas prête à cette époque à accepter de nouvelles idées de quelque nature que ce soit. L’acceptation a été lente, même aussi tard que le XVe siècle lorsque les mathématiques européennes ont commencé son développement rapide qui continue aujourd’hui. Nous n’examinerons pas dans cet article les nombreuses contributions à l’introduction du système de numérotation Indien en Europe, mais nous terminerons par un seul exemple qui, cependant, est très important., Fibonacci écrit dans son célèbre livre Liber abaci published publié à Pise en 1202: –
quand mon père, qui avait été nommé par son pays comme notaire public à la douane de Bugia agissant pour les marchands Pisans qui s’y rendaient, était en charge, il m’a convoqué auprès de lui alors que j’étais encore enfant, et ayant un œil sur l’utilité et la commodité future, a souhaité que j’y reste et reçoive une instruction à l’école de comptabilité., Là, quand j’avais été initié à l’art des neuf symboles Indiens par un enseignement remarquable, la connaissance de l’art m’a très vite plu par-dessus tout et j’en suis venu à le comprendre, car tout ce qui a été étudié par l’art en Égypte, en Syrie, en Grèce, en Sicile et en Provence, sous toutes ses formes.