algoritmi de sortare sunt modalități de a organiza o serie de elemente de la cel mai mic la cel mai mare. Acești algoritmi pot fi utilizați pentru a organiza date dezordonate și pentru a facilita utilizarea. În plus, înțelegerea acestor algoritmi și modul în care funcționează este fundamentală pentru o înțelegere puternică a informaticii, care devine din ce în ce mai critică într-o lume a pachetelor premade. Acest blog se concentrează pe viteza, utilizările, avantajele și dezavantajele algoritmilor de sortare specifici.,deși există o mare varietate de algoritmi de sortare, acest blog explică inserarea dreaptă, Sortare coajă, Sortare bule, sortare rapidă, Sortare selecție și sortare grămadă. Primii doi algoritmi (Straight Insertion și Shell Sort) sortează matricele cu inserție, care este atunci când elementele sunt introduse în locul potrivit. Următoarele 2 (sortare cu bule și sortare rapidă) sortează matricele cu schimbul, care este atunci când elementele se mișcă în jurul matricei. Ultimul este heap sort care sortează prin selecție unde elementele potrivite sunt selectate pe măsură ce algoritmul rulează în jos.,
notație Big-O
înainte ca acest blog să meargă mai departe, este esențial să explicăm metodele pe care profesioniștii le folosesc pentru a analiza și evalua complexitatea și performanța algoritmilor. Standardul actual se numește ” mare o notație „numit în funcție de notația sa, care este un” O „urmată de o funcție, cum ar fi” o(n).”
definiție formală
Big O este folosit pentru a desemna fie complexitatea de timp a unui algoritm sau cât de mult spațiu este nevoie. Acest blog se concentrează în principal pe partea de complexitate a timpului acestei notații., Modul în care oamenii pot calcula acest lucru este prin identificarea celui mai rău caz pentru algoritmul vizat și formularea unei funcții a performanței sale, având în vedere o cantitate n de elemente. De exemplu, dacă ar exista un algoritm care a căutat numărul 2 într-o matrice, atunci cel mai rău caz ar fi dacă 2 ar fi la sfârșitul matricei. Prin urmare, notația mare O ar fi O(n), deoarece ar trebui să treacă prin întreaga matrice de elemente n înainte de a găsi numărul 2.pentru a vă ajuta, găsiți mai jos un tabel cu algoritmi și complexitatea acestuia.,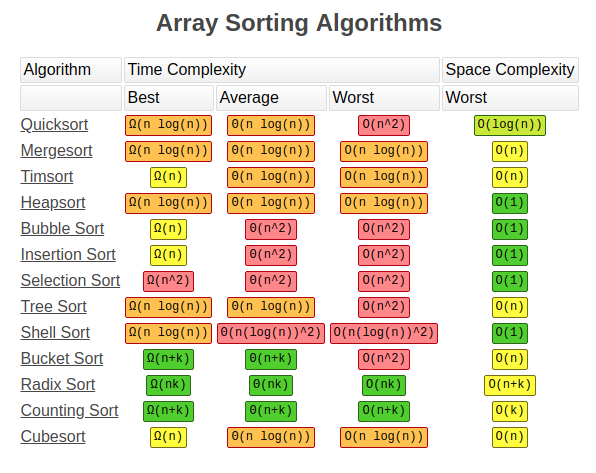
Drept un Fel de introducere

Drept un fel de inserare este una dintre cele mai de bază algoritmi de sortare care, în esență, introduce un element în poziția corectă de o listă deja sortate. Acesta este de obicei adăugat la sfârșitul unui nou tablou și se deplasează în jos până când găsește un element mai mic mulțumesc în sine (poziția dorită). Procesul se repetă pentru toate elementele din matrice nesortate. Luați în considerare matricea {3,1,2,5,4}, începem de la 3 și, deoarece nu există alte elemente în matricea sortată, matricea sortată devine doar {3}., După aceea, introducem 1 Care este mai mic decât 3, așa că s-ar mișca în fața lui 3 făcând matricea {1,3}. Același proces se repetă pe linie până când obținem matricea {1,2,3,4,5}.
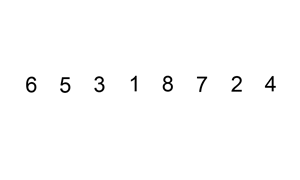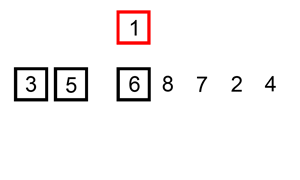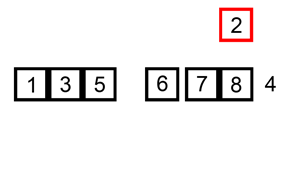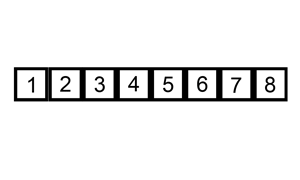
avantajele acestui proces sunt că este simplu și ușor de implementat. De asemenea, este relativ rapid atunci când există cantități mici de elemente pentru a sorta. Se poate transforma, de asemenea, în inserție binară, care este atunci când comparați pe distanțe mai lungi și restrângeți-o până la locul potrivit, în loc să comparați fiecare element înainte de locul potrivit., Cu toate acestea, un fel de inserție dreaptă este de obicei lent ori de câte ori lista devine mare.
Caracteristici Principale:
- un fel de introducere de familie
- simplu și simplu
- mai Rău caz = O(n^2)
implementare Python:
Shell Sort
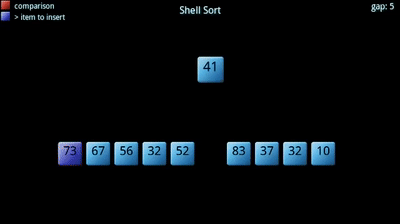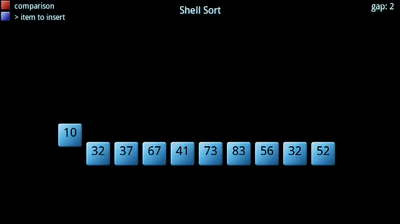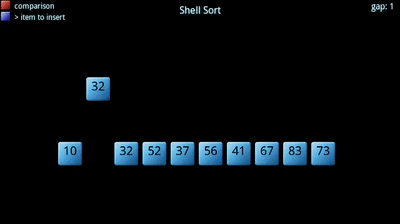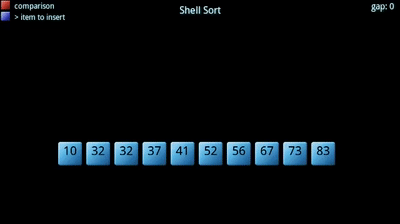
Shell sort este un fel de introducere prima parțial felul său de date și apoi se termină la fel executând un fel de introducere algoritm pe întreaga matrice. Acesta începe, în general, prin alegerea subseturi mici de matrice și sortarea acestor matrice., După aceea, repetă același proces cu subseturi mai mari până când ajunge la un punct în care subsetul este matricea și întregul lucru devine sortat. Avantajul de a face acest lucru este că având matrice aproape în întregime sortate ajută inserarea finală fel atinge sau să fie aproape de scenariul său cel mai eficient.
În plus, creșterea dimensiunii subseturilor se realizează printr-un termen de creștere descrescătoare. Termenul increment alege, în esență, fiecare element kth pentru a pune în subset., Acesta începe mare, ceea ce duce la grupuri mai mici (mai răspândit), și devine mai mică până când devine 1 (Toate matrice).principalul avantaj al acestui algoritm de sortare este că este mai eficient decât un fel de inserare obișnuit. De asemenea, există o varietate de algoritmi diferiți care încearcă să optimizeze sortarea shell-ului schimbând modul în care incrementul scade, deoarece singura restricție este că ultimul termen din secvența de incremente este 1. Cea mai populară este de obicei metoda lui Knuth care folosește formula h=((3^k)-1)/2,oferindu-ne o secvență de intervale de 1 (k=1), 4 (k=2), 13 (k=3) și așa mai departe., Pe de altă parte, shell sort nu este la fel de eficient ca alți algoritmi de sortare, cum ar fi quicksort și merge sort.
Caracteristici Principale:
- Sortarea prin inserție
- Poate optimiza algoritmul de schimbare trepte
- Utilizarea Knuth metoda lui, cazul cel mai nefavorabil este O(n^(3/2))
implementare Python:
Bubble Sort
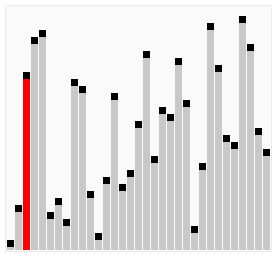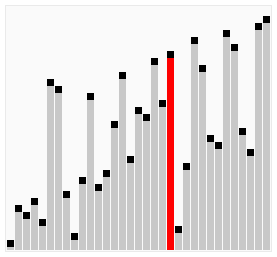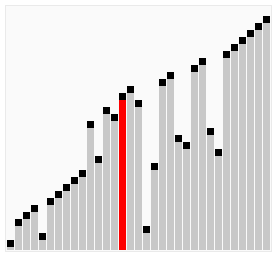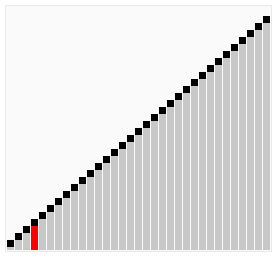
sortare cu Bule compară elemente adiacente ale unei matrice și organizează aceste elemente. Numele său provine din faptul că un număr mare tind să „plutească” (bule) în partea de sus., Se bucle printr-o matrice și vede dacă numărul de la o poziție este mai mare decât numărul în poziția următoare, ceea ce ar duce la numărul se deplasează în sus. Acest ciclu se repetă până când algoritmul a trecut prin matrice fără a fi nevoie să schimbați ordinea. Această metodă este avantajoasă deoarece este simplă și funcționează foarte bine pentru listele sortate în cea mai mare parte. Drept urmare, programatorii pot implementa rapid și ușor acest algoritm de sortare. Cu toate acestea, compromisul este că acesta este unul dintre algoritmii de sortare mai lenți.,
Caracteristici Principale:Schimb sortingEasy să implementWorst Caz = O(n^2)
Python aplicare:
Quicksort
Quicksort este una dintre cele mai eficiente algoritmi de sortare, iar acest lucru face din ea una dintre cele mai folosite la fel de bine.Primul lucru de făcut este să selectați un număr pivot, acest număr va separa datele, în stânga sunt numerele mai mici decât acesta și numerele mai mari din dreapta. Cu aceasta, am împărțit întreaga secvență.,După ce datele sunt partiționate, putem asigura că partițiile sunt orientate, știm că avem valori mai mari în dreapta și valori mai mici în stânga.Quicksort folosește acest algoritm divide și conquer cu recursivitate. Deci, acum că avem datele împărțite, folosim recursivitatea pentru a apela aceeași metodă și a trece jumătatea stângă a datelor, iar după jumătatea dreaptă pentru a continua separarea și ordonarea datelor. La sfârșitul execuției, vom avea toate datele sortate.,
caracteristici Principale:
- Din familia de Schimb de Sortare Algoritmi
- Divide și cuceri paradigmă
- cel mai Rău caz, de complexitate O(n2)
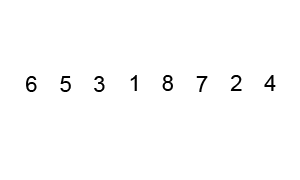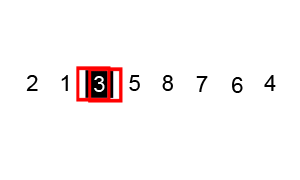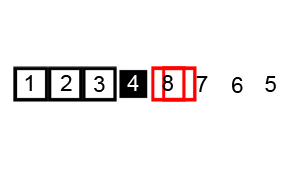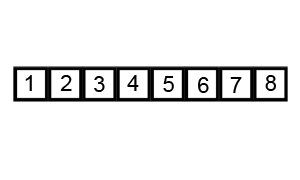
implementare Python:
Heapsort
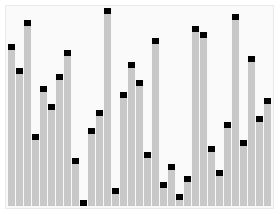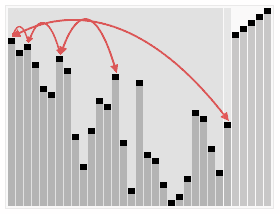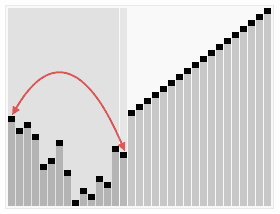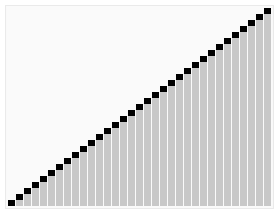
Heapsort este un algoritm de sortare bazat în structura de heap. Heap este o structură de date specializată găsită într-un copac sau un vector.In prima etapă a algoritmului, un copac este creat cu valorile care urmează să fie sortate, pornind de la stânga, vom crea nodul rădăcină, cu prima valoare., Acum creăm un nod copil stâng și introducem următoarea valoare, în acest moment evaluăm dacă valoarea setată la nodul copil este mai mare decât valoarea de la nodul rădăcină, dacă da, schimbăm valorile. Facem asta la tot copacul. Ideea inițială este că nodurile părinte au întotdeauna valori mai mari decât nodurile copil.la sfârșitul primului pas, creăm un vector începând cu valoarea rădăcină și mergând de la stânga la dreapta umplând vectorul.,acum începem să comparăm valorile nodurilor părinte și copil care caută cea mai mare valoare între ele, iar când o găsim, schimbăm locurile reordonând valorile. În primul pas, comparăm nodul rădăcină cu ultima frunză din copac. Dacă nodul rădăcină este mai mare, atunci schimbăm valorile și continuăm să repetăm procesul până când ultima frunză este valoarea mai mare. Când nu mai există valori de rearanjat, adăugăm ultima frunză la vector și repornim procesul. Putem vedea acest lucru în imaginea de mai jos.,

principalele caracteristici ale algoritmului sunt:
- Din familia de sortare prin selecție
- Comparații, în cel mai rău caz = O(n log n)
- Nu stabile
implementare Python:
de Referință: Cât de repede sunt?
după dezvoltarea algoritmilor este bine pentru noi să testăm cât de repede pot fi. În această parte am dezvoltat un program simplu folosind codul de mai sus pentru a genera un benchmark de bază, doar pentru a vedea cât timp pot folosi pentru a sorta o listă de numere întregi.,Observații importante despre Cod:
- Python limita implicită de apel de recursiune este de 1.000, în acest test folosim numere mari, așa că a trebuit să îmbunătățim acel număr pentru a rula benchmark-ul fără erori. Limita a fost stabilită la 10.000.
- acest cod măsoară doar timpul de funcționare al fiecărui algoritm.
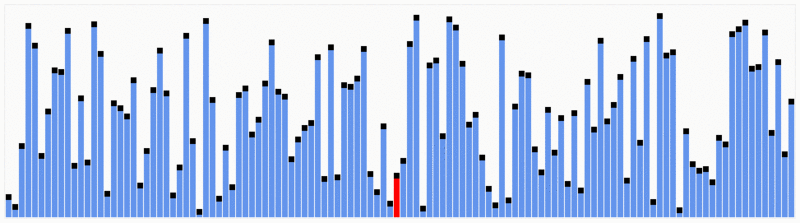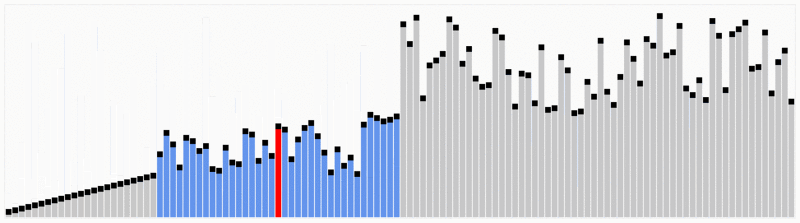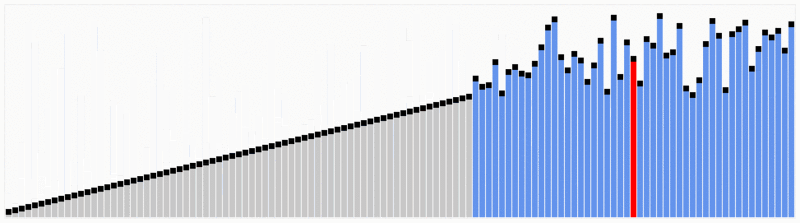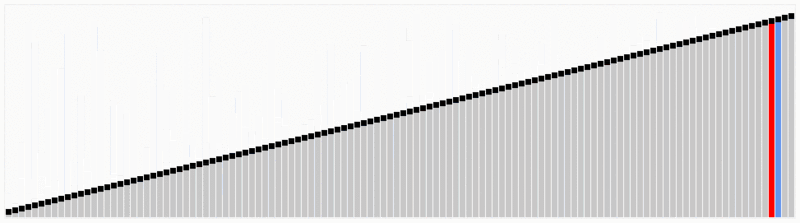
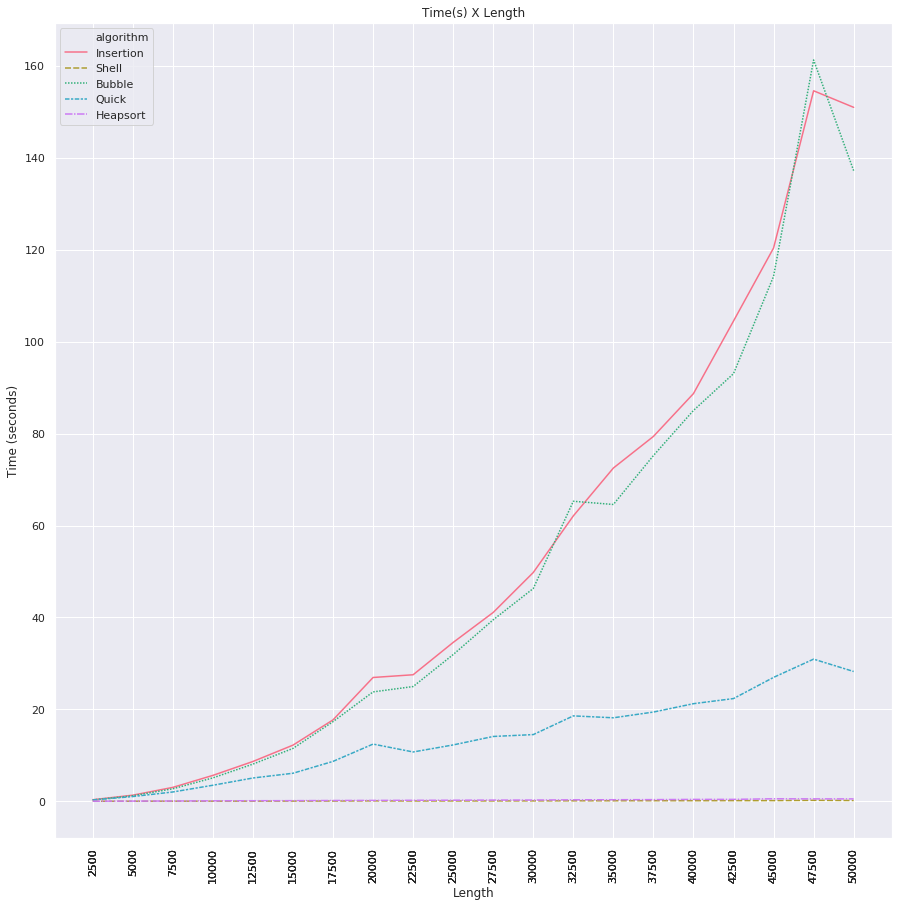
- s-au făcut 20 de teste cu dimensiuni diferite de liste variind de la 2500 la 50000.numerele au fost generate randonly variind de la 1 la 10000.,Rezultatele sunt următoarele: Shell sort și Heap algoritmi de sortare efectuate bine în ciuda lungimii listelor, în cealaltă parte am constatat că Sortare inserție și algoritmi de sortare cu bule au fost mult mai rău, crescând în mare măsură timpul de calcul. Vedeți rezultatele din graficul de mai jos.
concluzie
în această postare, am arătat 5 dintre cei mai comuni algoritmi de sortare utilizați astăzi. Înainte de a utiliza oricare dintre ele este extrem de important să se știe cât de repede se execută și cât de mult spațiu se va folosi. Deci este compromisul dintre complexitate, viteză și volum., O altă caracteristică critică a algoritmilor de sortare care sunt importante de știut este stabilitatea sa. Stabilitatea înseamnă că algoritmul păstrează ordinea elementelor cu valori cheie egale. Cel mai bun algoritm se schimbă pentru fiecare set diferit de date și, ca rezultat, înțelegerea datelor noastre joacă un rol semnificativ în procesul de alegere a algoritmului potrivit.după cum putem vedea, înțelegerea datelor noastre joacă un rol foarte important în procesul de alegere a algoritmului potrivit.,dacă această postare v-a atras atenția, aruncați o privire la videoclipul de mai jos, vă va oferi o explicație concisă despre 15 algoritmi de sortare.

O Notație Mare – https://en.wikipedia.org/wiki/Big_O_notation
Knuth, Donald Ervin, 1938 – The art of computer programming / Donald Ervin Knuth. xiv, 782 p. 24 cm.,d=”a5b60f8536″>
Quicksort – https://commons.wikimedia.org/wiki/File:Quicksort.gif
Quicksort – http://interactivepython.org/courselib/static/pythonds/SortSearch/TheQuickSort.html
Heapsort Algorithm – https://en.wikipedia.org/wiki/Heapsort
Heapsort Algorithm – https://www.geeksforgeeks.org/heap-sort/
Bubble sort – http://interactivepython.org/runestone/static/pythonds/SortSearch/TheBubbleSort.html
Sedgewick, R.,, & Wayne, K. (2011). Algorithms, 4th Edition. (p. I–XII, 1-955). Addison-Wesley. – https://algs4.cs.princeton.edu/20sorting/
Sorting algorithms – https://brilliant.org/wiki/sorting-algorithms/