funcția de distribuție Poisson

distribuția Poisson oferă o modalitate utilă de a evalua procentul de timp în care se așteaptă un anumit interval de rezultate. S-ar putea dori să proiecteze o limită superioară rezonabilă pe un eveniment după ce a făcut o serie de observații.,

De exemplu, dacă ați măsurat un anumit tip de eveniment special, doar o singură dată (x=1) în timpul rula dumneavoastră la o mare accelerator după observarea n evenimente, atunci ați putea dori să-proiect cât de multe evenimente ar trebui să respecte pentru a avea o 90% nivel de încredere de cel puțin încă un astfel de eveniment special. (Acest lucru ar ajuta apăra cererea dumneavoastră pentru mai mult timp pe accelerator data viitoare!) Acest tip de proiecție este foarte potrivit pentru Statisticile Poisson., O abordare convenabilă a calculului este de a calcula valoarea medie ” a ” a observației pentru care observarea valorii x=0 este probabilă de 10%. În ceea ce privește distribuția Poisson, această condiție poate fi exprimată ca

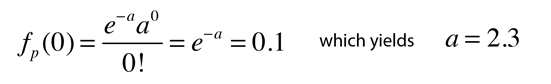
Acum, deoarece media este un = n ‘ p și probabilitatea p=1/n unde n este numărul de observații anterioare, rezultă că pentru a atinge 90% nivel de încredere de a vedea un alt eveniment special, ar trebui să observați n’ = 2.3 n mai multe evenimente. Adică trebuie să observați 2.,De 3 ori mai multe decât ați făcut prima dată pentru a fi 90% sigur că veți vedea altul.

un Alt mod de a interpreta acest rezultat este că, dacă respectați n evenimente, fără să vadă nici de dorit evenimente speciale, apoi cu încredere de 90% se poate spune că valoarea medie pentru observarea unor astfel de evenimente este mai mică de 2,3 = a, unde a=np este standard valoarea medie. Pe baza unui număr mic de observații ale evenimentelor care se presupune că acționează prin probabilitate pură, puteți face o proiecție a limitei superioare pentru astfel de evenimente la un nivel ales de încredere.,