Introduction to Survival Analysis: the Kaplan-Meier estimator (Română)

în articolul meu anterior, am descris potențialele cazuri de utilizare a analizei de supraviețuire și am introdus toate blocurile necesare pentru a înțelege tehnicile utilizate pentru analizarea datelor time-to-event.continuăm seria explicând probabil cea mai simplă, dar foarte profundă abordare a analizei supraviețuirii — Estimatorul Kaplan-Meier. După o introducere teoretică, vă voi arăta cum să efectuați analiza în Python folosind biblioteca populară lifetimes.,Estimatorul Kaplan-Meier (cunoscut și ca Estimatorul limită de produs, veți vedea de ce mai târziu) este o tehnică non-parametrică de estimare și trasare a probabilității de supraviețuire în funcție de timp. Este adesea primul pas în efectuarea analizei de supraviețuire, deoarece este cea mai simplă abordare și necesită cele mai puține ipoteze. Pentru a efectua analiza folosind abordarea Kaplan-Meier, presupunem următoarele:

• evenimentul de interes este neechivoc și se întâmplă la un moment clar specificat.,
• probabilitatea de supraviețuire a tuturor observațiilor este aceeași, nu contează exact când au intrat în studiu.
• observațiile cenzurate au aceleași perspective de supraviețuire ca și observațiile care continuă să fie urmate.

în cazurile din viața reală, nu cunoaștem niciodată adevărata funcție de supraviețuire. De aceea, cu Estimatorul Kaplan-Meier, aproximăm adevărata funcție de supraviețuire din datele colectate.,tor este definită ca fracție de observații care au supraviețuit pentru o anumită perioadă de timp, în aceleași circumstanțe, și este dat de următoarea formulă:

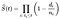
în cazul în care:

• t_i este un moment în care cel puțin un eveniment s-a întâmplat,
• d_i este numărul de evenimente care s-au întâmplat în timp t_i,
• n_i reprezintă numărul de persoane cunoscute, a supraviețuit până la data t_i (încă nu au avut moarte eveniment sau au fost cenzurate)., Sau altfel spus, numărul de observații la risc la momentul t_i.

Din produsul simbol în formula, putem vedea conectarea la alte nume de metodă, produs-limită de estimator. Probabilitatea de supraviețuire la momentul t este egală cu produsul șanselor procentuale de supraviețuire la momentul t și de fiecare dată anterioară.ceea ce asociem cel mai adesea cu această abordare a analizei supraviețuirii și ceea ce vedem în general în practică sunt curbele Kaplan-Meier — un complot al estimatorului Kaplan-Meier în timp., Putem folosi aceste curbe ca instrument de explorare — pentru a compara funcția de supraviețuire între cohorte, grupuri care au primit un fel de tratament sau nu, grupuri comportamentale etc.

supraviețuirea linie este de fapt o serie de scădere orizontală etape, care se apropie de forma a populației este adevărat supraviețuire funcția dat un eșantion suficient de mare., În practică, complotul este adesea însoțit de intervale de încredere, pentru a arăta cât de incert suntem cu privire la estimările punctuale — intervalele de încredere largi indică o incertitudine ridicată, probabil datorită studiului care conține doar câțiva participanți — cauzate de ambele observații moarte și cenzurate. Pentru mai multe detalii privind calculul intervalelor de încredere folosind metoda Greenwood, vă rugăm să consultați .,

interpretarea de curba de supraviețuire este destul de simplu, axa y reprezintă probabilitatea ca subiectul încă nu a experimentat eveniment de interes după ce a supraviețuit până la momentul t, reprezentată pe axa x. Fiecare scădere a funcției de supraviețuire (aproximată de Estimatorul Kaplan-Meier) este cauzată de evenimentul de interes care se întâmplă pentru cel puțin o observație.,

lungimea reală a liniei verticale reprezintă fracțiunea de observații la risc care au experimentat evenimentul la momentul t. aceasta înseamnă că o singură observație (nu de fapt aceeași, ci pur și simplu singulară) care se confruntă cu evenimentul în două momente diferite poate duce la o scădere a dimensiunii diferenței — în funcție de numărul de observații la risc. În acest fel, înălțimea picăturii ne poate informa și despre numărul de observații cu risc (chiar și atunci când nu sunt raportate și/sau nu există intervale de încredere).,

când nici o observație nu a experimentat evenimentul de interes sau unele observații au fost cenzurate, nu există nicio scădere a curbei de supraviețuire.

log-rank test

Am învățat cum să utilizați Kaplan-Meier estimator pentru a aproxima adevărat funcția de supraviețuire a unei populații., Și știm că putem trasa mai multe curbe pentru a compara formele lor, de exemplu, prin sistemul de operare pe care îl folosesc utilizatorii aplicației noastre mobile. Cu toate acestea, încă nu avem un instrument care să permită compararea. Ei bine, cel puțin unul mai riguros decât eyeballing curbele.

aceasta este atunci când testul log-rank intră în joc. Este un test statistic care compară probabilitățile de supraviețuire între două grupuri (sau mai multe, pentru că vă rugăm să consultați Implementarea Python). Ipoteza nulă a testului afirmă că nu există nicio diferență între funcțiile de supraviețuire ale grupurilor considerate.,

testul log-rank utilizează aceleași ipoteze ca și Estimatorul Kaplan-Meier. În plus, există ipoteza proporțională a pericolelor — rata de pericol (vă rugăm să consultați articolul precedent pentru a vă reaminti despre rata de pericol) ar trebui să fie constantă pe toată perioada studiului. În practică, acest lucru înseamnă că testul log-rank ar putea să nu fie un test adecvat dacă curbele de supraviețuire se încrucișează. Cu toate acestea, acesta este încă un subiect de dezbatere activă, vă rugăm să consultați și .

pentru concizie, nu acoperim matematica din spatele testului. Dacă sunteți interesat, vă rugăm să consultați acest articol sau .,

greșeli comune cu Kaplan-Meier

în această parte, am vrut să menționez câteva dintre greșelile comune care pot apărea în timp ce lucrați cu Estimatorul Kaplan-Meier.

eliminarea datelor cenzurate

ar putea fi tentant să eliminați datele cenzurate, deoarece pot modifica semnificativ forma curbei Kaplan-Meier, cu toate acestea, acest lucru poate duce la prejudecăți severe, așa că ar trebui să o includem întotdeauna în timp ce se potrivește modelului.,

Interpretarea capetele de curbe

se Acorde o atenție specială atunci când se interpretează sfârșitul curbele de supraviețuire, ca orice mare scade aproape de sfârșitul studiului poate fi explicat prin doar câteva observații ajunge la acest moment de timp (acest lucru ar trebui să fie, de asemenea, indicat printr-un larg interval de încredere)

Dichotomizing variabile continue

De dichotomizing adică folosind mediana sau „optim” cut-off punct pentru a crea grupuri, cum ar fi „low” și „high” cu privire la orice continuu metric., Această abordare poate crea multiple probleme: găsirea unui punct de separare „optim” poate fi foarte dependentă de setul de date și imposibil de reprodus în diferite studii. De asemenea, făcând comparații multiple, riscăm să creștem șansele de fals pozitive (găsirea unei diferențe în funcțiile de supraviețuire, când de fapt nu există).

Dichotomizarea scade puterea testului statistic prin forțarea tuturor măsurătorilor la o valoare binară, ceea ce la rândul său poate duce la necesitatea unei dimensiuni mult mai mari a eșantionului necesară pentru detectarea unui efect., De asemenea, merită menționat faptul că, prin analiza supraviețuirii, dimensiunea eșantionului necesar se referă la numărul de observații cu evenimentul de interes.

când dihotomizăm, facem presupuneri slabe cu privire la distribuția riscului între observații. Să presupunem că folosim vârsta de 50 de ani ca împărțirea între pacienții tineri și bătrâni. Dacă facem acest lucru, presupunem că un tânăr de 18 ani se află în același grup de risc ca un copil de 49 de ani, ceea ce nu este adevărat în majoritatea cazurilor.,

contabilizarea unui singur predictor

Estimatorul Kaplan-Meier este o metodă univariabilă, deoarece aproximează funcția de supraviețuire folosind cel mult o variabilă/predictor. Drept urmare, rezultatele pot fi ușor părtinitoare — fie exagerează, fie lipsesc semnalul. Aceasta este cauzată de așa-numita prejudecată variabilă omisă, care determină analiza să presupună că efectele potențiale ale mai multor predictori ar trebui atribuite numai celui unic, pe care îl luăm în considerare. Din acest motiv, ar trebui utilizate metode multivariabile, cum ar fi regresia Cox.,

exemplu în Python

este timpul să implementăm ceea ce am învățat în practică. Începem prin importul tuturor bibliotecilor necesare.

Apoi, ne-am încărca setul de date și de a face unele mici certuri pentru a face să funcționeze bine cu frânghii de bibliotecă. Pentru analiză, folosim popularul set de date Telco pentru clienți (disponibil aici sau pe GitHub-ul meu)., Setul de date conține informații despre clienți ale unui furnizor de telefonie / internet, inclusiv mandatul acestora, ce fel de servicii utilizează, unele date demografice și, în cele din urmă, steagul care indică putină.,

Pentru această analiză, vom folosi următoarele coloane:

• tenure — numărul de luni în care clientul a rămas cu compania,
• churn — informații dacă clientul churned (binar codificat: 1 dacă evenimentul s-a întâmplat, 0 în caz contrar),
• PaymentMethod— ce fel de metodă de plată clienților folosit.,

pentru scenariul cel mai de bază, avem nevoie doar de timpul până la eveniment și de steagul care indică dacă s-a întâmplat evenimentul de interes.

KaplanMeierFitter funcționează în mod similar la clasele cunoscut din scikit-learn: prima instantiate de obiectul de clasă și de a folosi apoi fit metoda pentru a se potrivi modelul nostru de date., În timp ce trasăm, specificăm at_risk_counts=True pentru a afișa suplimentar informații despre numărul de observații expuse riscului în anumite momente de timp.

în mod Normal, ne-ar fi interesat în timpul median de supraviețuire, care este, la momentul în care, în medie, 50% din populație a murit deja, sau în acest caz, churned., Putem accesa folosind următoarea linie:

kmf.median_survival_time_

cu toate Acestea, în acest caz, comanda se întoarce inf, după cum putem vedea din curba de supraviețuire că facem de fapt nu observa că punctul nostru de date.am văzut cazul de utilizare de bază, acum să complicăm analiza și să trasăm curbele de supraviețuire pentru fiecare variantă a metodei de plată., Putem face acest lucru prin rularea următorul cod:

se Execută blocul de cod generează următoarele complot:

Putem vedea că probabilitatea de supraviețuire este cu siguranta cel mai mic pentru cec electronic, în timp ce curbele pentru automate de transfer bancar/card de credit sunt foarte similare., Acesta este un moment perfect pentru a utiliza testul log-rank pentru a vedea dacă acestea sunt de fapt diferite.

tabelul următor prezintă rezultatele.

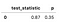
uitandu-se la p-valoarea de 0,35, putem vedea că nu există motive pentru a respinge ipoteza nulă să ateste că supraviețuirea funcții sunt identice. Pentru acest exemplu, am comparat doar două metode de plată., Cu toate acestea, există cu siguranță mai multe combinații pe care le-am putea testa. Există o funcție la îndemână numită pairwise_logrank_test, ceea ce face comparația foarte ușoară.

În masă, vom vedea comparația anterioară am făcut-o, precum și toate celelalte combinații. Transferul bancar vs, cardul de credit este singurul caz în care nu ar trebui să respingem ipoteza nulă. De asemenea, ar trebui să fim atenți la interpretarea rezultatelor testului log-rank, așa cum putem vedea în complotul de mai sus că curbele pentru plățile prin transfer bancar și prin card de credit se încrucișează, astfel încât presupunerea pericolelor proporționale este încălcată.există încă două lucruri pe care le putem testa cu ușurință folosind biblioteca lifelines. Primul este testul multivariat log-rank, în care ipoteza nulă afirmă că toate grupurile au același proces de generare a „morții”, astfel încât curbele lor de supraviețuire sunt identice.,

rezultatele testului indică faptul că ar trebui să respingem ipoteza nulă, deci curbele de supraviețuire nu sunt identice, pe care le-am văzut deja în teren.în cele din urmă, putem testa diferența de supraviețuire la un anumit moment în timp. Revenind la exemplu, în complot, putem vedea că curbele sunt cele mai îndepărtate în jurul valorii de t = 60., Să vedem dacă această diferență este semnificativă statistic.

uitându-ne la testul p-valoare, nu există niciun motiv pentru a respinge ipoteza nulă să ateste că nu există nici o diferență între supraviețuirea la acel moment de timp.

concluzii

În acest articol, am descris un instrument foarte popular pentru efectuarea analizei de supraviețuire — Estimatorul Kaplan-Meier., De asemenea, am acoperit testul log-rank pentru compararea a două/mai multe funcții de supraviețuire. Abordarea descrisă este una foarte populară, însă nu fără defecte. Înainte de a încheia, să aruncăm o privire la avantajele și dezavantajele estimatorului/curbelor Kaplan-Meier.

avantaje:

• oferă o vedere medie a populației, de asemenea pe grupuri.
• nu are nevoie de o mulțime de caracteristici — doar informații despre timp-to-eveniment și în cazul în care evenimentul a avut loc de fapt. În plus, putem folosi orice caracteristici categorice care descriu grupuri.,
• gestionează automat dezechilibrul clasei, deoarece practic orice proporție de deces la evenimentele cenzurate este acceptabilă.
• deoarece este o metodă non-parametrică, se fac puține ipoteze cu privire la distribuția subiacentă a datelor.

dezavantaje:

• Nu putem evalua amploarea impactului predictorului asupra probabilității de supraviețuire.
• nu putem ține cont simultan de mai mulți factori pentru observații, de exemplu, țara de origine și sistemul de operare al telefonului.,
• asumarea Independenței între cenzurare și supraviețuire (la momentul t, observațiile cenzurate ar trebui să aibă același prognostic ca și cele fără cenzurare) poate fi inaplicabilă/nerealistă.
• când distribuția de date subiacentă este (într-o oarecare măsură) cunoscută, abordarea nu este la fel de exactă ca unele tehnici concurente.rezumând, chiar și cu câteva dezavantaje, curbele de supraviețuire Kaplan-Meier sunt un loc minunat pentru a începe în timp ce efectuați analiza de supraviețuire., În timp ce facem acest lucru, putem obține informații valoroase despre potențialii predictori ai supraviețuirii și putem accelera progresul nostru cu câteva tehnici mai avansate (pe care le voi descrie în articolele viitoare).

  puteți găsi codul folosit pentru acest articol pe GitHub meu. Ca întotdeauna, orice feedback constructiv este binevenit. Puteți ajunge la mine pe Twitter sau în comentarii.în cazul în care vi se pare interesant acest articol, s-ar putea să vă placă și celelalte din serie:

  S. Sawyer (2003)., Intervalele de încredere Greenwood și Greenwood exponențiale în analiza supraviețuirii-disponibile aici

  curbele de supraviețuire Kaplan-Meier și testul Log-Rank-disponibile aici

  pericole neproporționale — deci ce? — disponibil aici

  Bouliotis, G., & Billingham, L. (2011). Traversarea curbelor de supraviețuire: alternative la testul log-rank. Studii, 12 (S1), A137.