rezolvarea ecuațiilor polinomiale de ordin superior este o abilitate esențială pentru oricine studiază știința și matematica. Cu toate acestea, înțelegerea modului de rezolvare a acestor ecuații este destul de dificilă.în acest articol, vom învăța cum rezolva ecuațiile cubice folosind diferite metode, cum ar fi metoda de divizare, Teorema factorului și factoring prin grupare. dar înainte de a intra în acest subiect, să discutăm ce este o ecuație polinomială și cubică.,un polinom este o expresie algebrică cu unul sau mai mulți termeni în care o constantă și o variabilă sunt separate printr-un semn de adunare sau scădere.forma generală a unui polinom este axn + bxn-1 + cxn – 2+…. + kx + l, unde fiecare variabilă are o constantă care o însoțește ca coeficient. Diferitele tipuri de polinoame includ; binomiale, trinomiale și quadrinomiale. Exemple de polinoame sunt; 3x + 1, x2 + 5xy – ax – 2ay, 6×2 + 3x + 2x + 1 etc.
o ecuație cubică este o ecuație algebrică de gradul trei.,
forma generală a unui cub este funcția: f (x) = ax3 + bx2 + cx1 + d. Și cubi ecuația are forma de ax3 + bx2 + cx + d = 0, unde a, b și c sunt coeficienți și d este constantă.
cum se rezolvă ecuațiile cubice?modul tradițional de rezolvare a unei ecuații cubice este de a o reduce la o ecuație pătratică și apoi de a rezolva fie prin factoring, fie prin formula pătratică.ca o ecuație pătratică are două rădăcini reale, o ecuație cubică poate avea, eventual, trei rădăcini reale., Dar, spre deosebire de ecuația pătratică, care poate avea nici o soluție reală, o ecuație cubică are cel puțin o rădăcină reală.celelalte două rădăcini pot fi reale sau imaginare.ori de câte ori vi se oferă o ecuație cubică sau orice ecuație, trebuie să o aranjați întotdeauna într-o formă standard.de exemplu, dacă vi se oferă ceva de genul acesta, 3×2 + x – 3 = 2/x, veți rearanja în formularul standard și îl veți scrie ca, 3×3 + x2-3x – 2 = 0. Apoi puteți rezolva acest lucru prin orice metodă potrivită.,să vedem câteva exemple de mai jos pentru o mai bună înțelegere:
Exemplul 1
determinați rădăcinile ecuației cubice 2×3 + 3×2 – 11x – 6 = 0
soluție
deoarece d = 6, atunci factorii posibili sunt 1, 2, 3 și 6.acum aplicați Teorema factorului pentru a verifica valorile posibile prin încercare și eroare.
(1) = 2 + 3 – 11 – 6 ≠ 0
f (-1) = -2 + 3 + 11 – 6 ≠ 0
f (2) = 16 + 12 – 22 – 6 = 0prin urmare, x = 2 este prima rădăcină.prin urmare, soluțiile sunt x = 2, x = -1/2 și x = -3.,
Exemplul 2
găsiți rădăcinile ecuației cubice x3 − 6×2 + 11x – 6 = 0
soluție
x3 − 6×2 + 11x – 6
(x – 1) este unul dintre factori.
Prin împărțirea x3 − 6×2 + 11x – 6 prin (x – 1),
⟹ (x – 1) (x2 – 5x + 6) = 0
⟹ (x – 1) (x – 2) (x – 3) = 0
Acest al cubi soluțiile ecuației sunt x = 1, x = 2 și x = 3.
Exemplul 3
rezolva x3 – 2×2 – x + 2
soluție
factorizează ecuația.
x3-2×2-x + 2 = x2 (x – 2) – (x – 2)
= (x2 – 1) (x – 2)
= (x + 1) (x – 1) (x – 2)
x = 1, -1 și 2.,
Example 4
Solve the cubic equation x3 – 23×2 + 142x – 120
Solution
First factorize the polynomial.
x3 – 23×2 + 142x – 120 = (x – 1) (x2 – 22x + 120)
But x2 – 22x + 120 = x2 – 12x – 10x + 120
= x (x – 12) – 10(x – 12)
= (x – 12) (x – 10)
Therefore, x3 – 23×2 + 142x – 120 = (x – 1) (x – 10) (x – 12)
Equate each factor to zero.
x – 1= 0
x = 1
x – 10 = 10
x – 12= 0
x = 12
The roots of the equation are x = 1, 10 and 12.
Example 5
Solve the cubic equation x3 – 6 x2 + 11x – 6 = 0.,pentru a rezolva această problemă folosind metoda divizării, luați orice factor al Constantei 6;
să x = 2
împărțiți polinomul cu x-2 la
(x2 – 4x + 3) = 0.
acum rezolva ecuația pătratică (x2-4x + 3) = 0 pentru a obține x= 1 sau x = 3
prin urmare, soluțiile sunt x = 2, x= 1 și x =3.
exemplul 6
rezolvați ecuația cubică x3 – 7X2 + 4x + 12 = 0
soluție
fie f(x) = x3 – 7X2 + 4x + 12
deoarece d = 12, valorile posibile sunt 1, 2, 3, 4, 6 și 12.,
prin încercare și eroare, constatăm că f (-1) = -1 – 7 – 4 + 12 = 0
deci, (x + 1) este un factor al funcției.
x3-7×2 + 4x + 12
= (x + 1) (x2 – 8x + 12)
= (x + 1) (x – 2) (x – 6)
prin urmare, x = -1, 2, 6
exemplul 7
rezolvați următoarea ecuație cubică:
x3 + 3×2 + x + 3 = 0.
soluție
x3 + 3×2 + x + 3
= (x3 + 3×2) + (x + 3)
= x2(x + 3) + 1(x + 3)
= (X + 3) (x2 + 1)
prin urmare, x = -1 ,1 -3.,
Example 8
Solve x3 − 6×2 + 11x − 6 = 0
Solution
Factorize
x3 − 6×2 + 11x − 6 = 0 ⟹ (x − 1) (x − 2) (x − 3) = 0
Equating each factor to zero gives;
x = 1, x = 2 and x = 3
Example 9
Solve x 3 − 4×2 − 9x + 36 = 0
Solution
Factorize each set of two terms.,ing fiecărui factor la zero, vom obține;
x = -3, 3 sau 4
Exemplu 10
Rezolva ecuația 3×3 −16×2 + 23x − 6 = 0
Soluție
Împărțiți 3×3 −16×2 + 23x – 6 x -2 pentru a obține 3×2 – 1 x – 9x + 3
= x (3x – 1) – 3(3x – 1)
= (x – 3) (3x – 1)
prin Urmare, 3×3 −16×2 + 23x − 6 = (x – 2) (x – 3) (3x – 1)
Echivala fiecare factor la zero pentru a obține,
x = 2, 3 și 1/3
Exemplu 11
de a Găsi rădăcinile de 3×3 – 3×2 – 90x=0
Soluție
factor l 3x
3×3 – 3×2 – 90x ⟹3x (x2 – x – 30)
Găsi o pereche de factori a căror produs este de -30 și suma este -1.,
⟹- 6 * 5 =-30
⟹ -6 + 5 = -1
rescrieți ecuația înlocuind termenul „bx” cu factorii aleși.
prin echivalarea fiecărui factor cu zero, obținem;
x= 0, 6, -5
rezolvarea ecuațiilor cubice folosind metoda grafică
dacă nu puteți rezolva ecuația cubică prin oricare dintre metodele de mai sus, o puteți rezolva cu ajutorul unei ecuații cubice.grafic. Pentru aceasta, trebuie să aveți o schiță exactă a ecuației cubice date.,
punctul (punctele) în care graficul său traversează axa x, este o soluție a ecuației. Numărul de soluții reale ale ecuațiilor cubice este același cu numărul de ori graficul său traversează axa X.
exemplul 12
găsiți rădăcinile x3 + 5×2 + 2x – 8 = 0 grafic.
Soluție
pur și Simplu desenați graficul de următoarea funcție, prin înlocuirea cu valori aleatoare x:
f (x) = x3 + 5×2 + 2x – 8
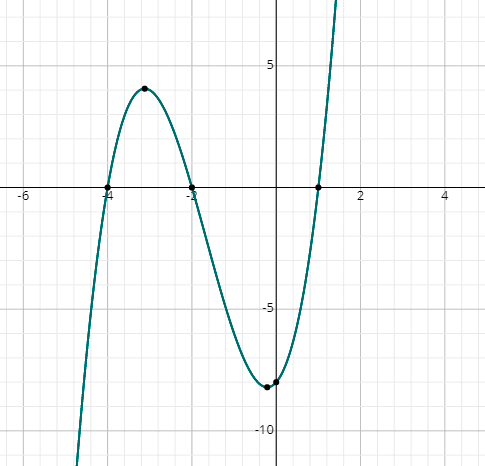
puteți vedea graficul taie axa x la 3 puncte, prin urmare, există 3 soluții reale.,
din grafic, soluțiile sunt:
x = 1, x = -2 & x = -4.
întrebări Practice
rezolvați următoarele ecuații cubice: