La desviación solo significa cuán lejos de la normal
desviación estándar
La desviación estándar es una medida de cómo se extienden los números.
Su símbolo es σ (la letra griega sigma)
La fórmula es fácil: es la raíz cuadrada de la Varianza. Así que ahora se preguntan, » ¿Cuál es la varianza?»
varianza
la varianza se define como:
el promedio de las diferencias cuadradas de la media.,
para calcular la varianza siga estos pasos:
- calcule la media (el promedio simple de los números)
- Luego para cada número: reste la media y cuadrar el resultado (la diferencia cuadrada).
- luego calcule el promedio de esas diferencias cuadradas. (¿Por Qué Cuadrado?)
ejemplo
usted y sus amigos acaban de medir las alturas de sus perros (en milímetros):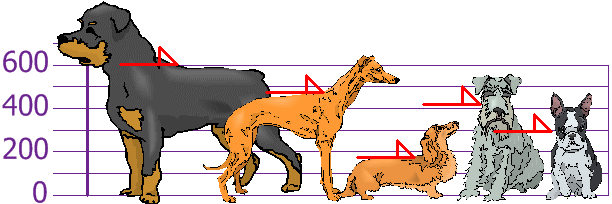
las alturas (en los hombros) son: 600mm, 470mm, 170mm, 430mm y 300mm.,
Find out the Mean, the Variance, and the Standard Deviation.
Your first step is to find the Mean:
Answer:
| Mean | = | 600 + 470 + 170 + 430 + 3005 |
| = | 19705 | |
| = | 394 |
so the mean (average) height is 394 mm.,2062 + 762 + (−224)2 + 362 + (−94)25
So the Variance is 21,704
And the Standard Deviation is just the square root of Variance, so:
| Standard Deviation | ||
| σ | = | √21704 |
| = | 147.,32… | |
| = | 147 (el más cercano mm) | |
Y la cosa buena acerca de la Desviación Estándar es que es útil. Ahora podemos mostrar qué alturas están dentro de una desviación estándar (147 mm) de la media: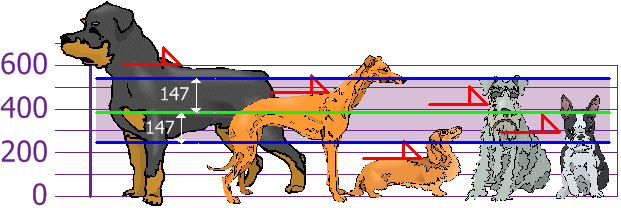
así, usando la desviación estándar tenemos una forma «estándar» de saber qué es normal, y qué es extra grande o extra pequeño.
los Rottweilers son perros altos. Y los salchichones son un poco cortos, ¿verdad?,
usando
podemos esperar que alrededor del 68% de los valores estén dentro de la desviación estándar plus-or-minus1.
lea distribución Normal estándar para obtener más información.
también Pruebe la calculadora de desviación estándar.
Pero … hay un pequeño cambio con los datos de la muestra
nuestro ejemplo ha sido para una población (los 5 perros son los únicos perros que nos interesan).
pero si los datos son una muestra (una selección tomada de una población más grande), entonces el cálculo cambia!,
cuando tiene » n » valores de datos que son:
- La población: dividir por N al calcular la varianza (como hicimos)
- Una muestra: dividir por N-1 al calcular la varianza
todos los demás cálculos permanecen iguales, incluida la forma en que calculamos la media.,
ejemplo: si nuestros 5 perros son solo una muestra de una población más grande de perros, dividimos por 4 en lugar de 5 de esta manera:
piense en ello como una «corrección» cuando sus datos son solo una muestra.,
Fórmulas
Aquí están las dos fórmulas, explicó en la Desviación Estándar de las Fórmulas si quieres saber más:
|
La «Desviación Estándar de Población»: |
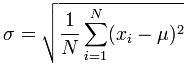 |
|
| La «Desviación Estándar»: | 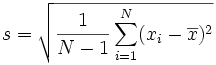 |
Parece complicado, pero el cambio importante es
dividir por N-1 (en lugar de N) la hora de calcular la Varianza de la Muestra.
