la prueba t se refiere a una prueba de hipótesis univariada basada en el estadístico t, en el que se conoce la media y la varianza poblacional se aproxima a partir de la muestra. Por otro lado, la prueba Z es también una prueba univariada que se basa en la distribución normal estándar.
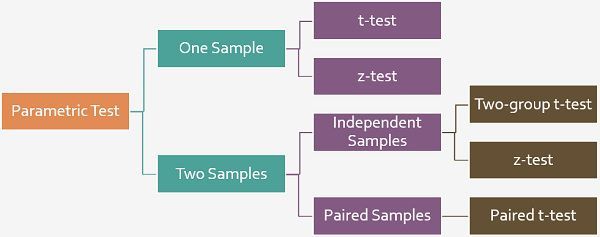
en términos simples, una hipótesis se refiere a una suposición que debe ser aceptada o rechazada. Hay dos procedimientos de prueba de hipótesis, i. e., Prueba paramétrica y prueba no paramétrica, en la que la Prueba paramétrica se basa en el hecho de que las variables se miden en una escala de intervalos, mientras que en la prueba no paramétrica, se asume que la misma se mide en una escala ordinal. Ahora, en la Prueba paramétrica, puede haber dos tipos de prueba, t-Prueba y z-prueba.
Este artículo le dará una comprensión de la diferencia entre la prueba T y la prueba Z en detalle.,
contenido: t-test Vs Z-test
- Comparison Chart
- Definition
- Key Differences
- Conclusion
Comparison Chart
| Basis para la comparación | t-test | Z-test |
|---|---|---|
| significado | t-test se refiere a un tipo de Prueba paramétrica que se aplica para identificar, cómo las medias de dos conjuntos de datos difieren entre sí cuando no se da la varianza., | la prueba Z implica una prueba de hipótesis que determina si las medias de dos conjuntos de datos son diferentes entre sí cuando se da la varianza., |
| Basado en | t-Student distribución | distribución Normal |
| la varianza de la Población | Desconocido | Conocido |
| Tamaño de la Muestra | Pequeño | Grande |
Definición de T-test
Un t-test es una prueba de hipótesis utilizadas por el investigador para comparar la población los medios para una variable, se clasifican en dos categorías dependiendo de la menos de intervalo variable., Más precisamente, se utiliza una prueba t para examinar cómo difieren las medias tomadas de dos muestras independientes.
la prueba t sigue la distribución t, que es apropiada cuando el tamaño de la muestra es pequeño y no se conoce la desviación estándar de la población. La forma de una distribución en t se ve muy afectada por el grado de libertad. El grado de libertad implica el número de observaciones independientes en un conjunto dado de observaciones.
suposiciones de la prueba T:
- Todos los puntos de datos son independientes.
- el tamaño de La muestra es pequeño., En general, un tamaño de muestra superior a 30 unidades de muestra se considera grande, de lo contrario pequeño, pero que no debe ser inferior a 5, para aplicar la prueba T.
- Los valores de muestra deben tomarse y registrarse con precisión.
el estadístico de la prueba es:
x es la media muestral
S es la desviación estándar muestral
n es el tamaño muestral
μ es la media poblacional
Prueba T pareada: una prueba estadística aplicada cuando las dos muestras son dependientes y se toman observaciones pareadas.,
definición de z-test
Z-test se refiere a un análisis estadístico univariado utilizado para probar la hipótesis de que las proporciones de dos muestras independientes difieren mucho. Determina hasta qué punto un punto de datos está lejos de su media del conjunto de datos, en desviación estándar.
el investigador adopta la prueba z, cuando se conoce la varianza poblacional, en esencia, cuando hay un gran tamaño de muestra, la varianza muestral se considera aproximadamente igual a la varianza poblacional., De esta manera, se supone que se conoce, a pesar del hecho de que solo se dispone de datos de muestra y, por lo tanto, se puede aplicar una prueba normal.
suposiciones de la prueba Z:
- Todas las observaciones de la muestra son independientes
- El tamaño de la muestra debe ser superior a 30.
- La distribución de Z es normal, con una media cero y varianza 1.,
la estadística de la prueba es:
x es la media de la muestra
σ es la desviación estándar de la población
n es el tamaño de la muestra
μ es la media de la población
diferencias clave entre la prueba T y la prueba Z
los siguientes motivos:
- la prueba t puede entenderse como una prueba estadística que se utiliza para comparar y analizar si las medias de las dos poblaciones son diferentes entre sí o no cuando se desconoce la desviación estándar., Por el contrario, Z-test es una Prueba paramétrica, que se aplica cuando se conoce la desviación estándar, para determinar, si las medias de los dos conjuntos de datos difieren entre sí.
- la prueba t se basa en la distribución T de Student. Por el contrario, la prueba z se basa en la suposición de que la distribución de las medias de la muestra es normal. Tanto la distribución t de student como la distribución normal parecen iguales, ya que ambas son simétricas y en forma de campana. Sin embargo, difieren en el sentido de que en una distribución t, hay menos espacio en el centro y más en las colas.,
- Una de las condiciones importantes para la adopción de la prueba t es que la varianza poblacional es desconocida. Por el contrario, la varianza de la población debe ser conocida o asumida como conocida en caso de una prueba Z.
- La prueba Z se utiliza para cuando el tamaño de la muestra es grande, es decir, n >30, y la prueba t es apropiada cuando el tamaño de la muestra es pequeño, en el sentido de que n < 30.,
conclusión
en general, la prueba t y la prueba z son pruebas casi similares, pero las condiciones para su aplicación son diferentes, lo que significa que la prueba t es apropiada cuando el tamaño de la muestra no es más de 30 unidades. Sin embargo, si es más de 30 unidades, se debe realizar la prueba Z. Del mismo modo, hay otras condiciones, lo que deja claro qué prueba se debe realizar en una situación dada.
