Introduction to Survival Analysis: the Kaplan-Meier estimator

en mi artículo anterior, describí los posibles casos de uso del análisis de supervivencia e introduje todos los bloques de construcción necesarios para comprender las técnicas utilizadas para analizar los datos de tiempo hasta el evento.

continúo la serie explicando quizás el enfoque más simple, pero muy perspicaz para el análisis de supervivencia: el estimador de Kaplan — Meier. Después de una introducción teórica, te mostraré cómo llevar a cabo el análisis en Python utilizando la Popular biblioteca lifetimes.,

el estimador de Kaplan-Meier (también conocido como estimador de límite de producto, verá por qué más adelante) es una técnica no paramétrica de estimación y trazado de la probabilidad de supervivencia en función del tiempo. A menudo es el primer paso para llevar a cabo el análisis de supervivencia, ya que es el enfoque más simple y requiere las menos suposiciones. Para llevar a cabo el análisis utilizando el enfoque de Kaplan-Meier, asumimos lo siguiente:

• El evento de interés es inequívoco y ocurre en un momento claramente especificado.,
• La probabilidad de supervivencia de todas las observaciones es la misma, no importa exactamente cuándo han entrado en el estudio.
• Las observaciones censuradas tienen las mismas perspectivas de supervivencia que las observaciones que continúan siendo seguidas.

en casos reales, nunca sabemos la verdadera función de supervivencia. Es por eso que con el estimador de Kaplan-Meier, aproximamos la verdadera función de supervivencia a partir de los datos recopilados.,tor se define como la fracción de observaciones que sobrevivieron durante un cierto tiempo bajo las mismas circunstancias y está dada por la siguiente fórmula:

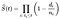
donde:

• t_i es un momento en el que ocurrió al menos un evento,
• d_i es el número de eventos que ocurrieron en el momento t_i,
• n_i representa el número de individuos que se sabe que han sobrevivido hasta el momento t_i (aún no han tenido el evento de muerte o han sido censurados)., O para decirlo de otra manera, el número de observaciones en riesgo en el tiempo t_i.

desde el símbolo del producto en la fórmula, podemos ver la conexión con el otro nombre del método, el estimador de límite de producto. La probabilidad de supervivencia en el tiempo t es igual al producto del porcentaje de probabilidad de supervivencia en el tiempo t y en cada tiempo anterior.

lo que más a menudo asociamos con este enfoque para el análisis de supervivencia y lo que generalmente vemos en la práctica son las curvas de Kaplan-Meier, una gráfica del estimador de Kaplan — Meier a lo largo del tiempo., Podemos usar esas curvas como una herramienta exploratoria-para comparar la función de supervivencia entre cohortes, grupos que recibieron algún tipo de tratamiento o no, grupos conductuales, etc.

la línea de supervivencia es en realidad una serie de pasos horizontales decrecientes, que se acercan a la forma de la verdadera función de supervivencia de la población dado un tamaño de muestra lo suficientemente grande., En la práctica, el gráfico a menudo se acompaña de intervalos de confianza, para mostrar cuán inciertos estamos sobre las estimaciones puntuales — los intervalos de confianza amplios indican una alta incertidumbre, probablemente debido al estudio que contiene solo unos pocos participantes — causada por ambas observaciones muriendo y siendo censuradas. Para obtener más detalles sobre el cálculo de los intervalos de confianza utilizando el método Greenwood, consulte .,

La interpretación de la curva de supervivencia es bastante simple, el eje y representa la probabilidad de que el tema aún no ha experimentado el evento de interés después de sobrevivir hasta el tiempo t, que se representa en el eje de las x. Cada caída en la función de supervivencia (aproximada por el estimador de Kaplan-Meier) es causada por el evento de interés que ocurre durante al menos una observación.,

la longitud real de la línea vertical representa la fracción de observaciones en riesgo que experimentaron el evento en el tiempo t. esto significa que una sola observación (no realmente la misma, sino simplemente singular) experimentando el evento en dos momentos diferentes puede resultar en una caída de tamaño de diferencia, dependiendo del número de observaciones en riesgo. De esta manera, la altura de la caída también puede informarnos sobre el número de observaciones en riesgo (incluso cuando no se reportan y/o no hay intervalos de confianza).,

Cuando ninguna observación experimentó el evento de interés o algunas observaciones fueron censuradas, no hay caída en la curva de supervivencia.

La prueba de log-rank

Hemos aprendido a utilizar el estimador de Kaplan-Meier para aproximarse a la verdadera función de sobrevivencia de una población., Y sabemos que podemos trazar múltiples curvas para comparar sus formas, por ejemplo, por el sistema operativo que usan los usuarios de nuestra aplicación móvil. Sin embargo, todavía no tenemos una herramienta que realmente permita la comparación. Bueno, al menos uno más riguroso que mirar las curvas.

es cuando entra en juego la prueba de rango logarítmico. Es una prueba estadística que compara las probabilidades de supervivencia entre dos grupos (o más, para eso consulte la implementación de Python). La hipótesis nula de la prueba establece que no hay diferencia entre las funciones de supervivencia de los grupos considerados.,

la prueba de rango logarítmico utiliza los mismos supuestos que el estimador de Kaplan-Meier. Además, existe el supuesto de riesgos proporcionales: la razón de riesgos (consulte el artículo anterior para obtener un recordatorio sobre la tasa de riesgos) debe ser constante durante todo el período de estudio. En la práctica, esto significa que la prueba de rango logarítmico podría no ser una prueba apropiada si las curvas de supervivencia se cruzan. Sin embargo, este sigue siendo un tema de debate activo, por favor ver y .

por brevedad, no cubrimos las matemáticas detrás de la prueba. Si está interesado, consulte este artículo o .,

errores comunes con Kaplan-Meier

en esta parte, quería mencionar algunos de los errores comunes que pueden ocurrir mientras se trabaja con el estimador de Kaplan-Meier.

Eliminar datos censurados

puede ser tentador eliminar datos censurados, ya que puede alterar significativamente la forma de la curva de Kaplan-Meier, sin embargo, esto puede conducir a sesgos severos, por lo que siempre debemos incluirlos mientras ajustamos el modelo.,

interpretación de los extremos de las curvas

preste especial atención al interpretar el final de las curvas de supervivencia, ya que cualquier caída grande cerca del final del estudio puede explicarse por solo unas pocas observaciones que alcanzan este punto de tiempo (esto también debe indicarse por intervalos de confianza más amplios)

Dicotomizar variables continuas

dicotomizar me refiero a usar la mediana o el punto de corte «óptimo» para crear grupos como «bajo» y «alto» con respecto a cualquier métrica continua., Este enfoque puede crear múltiples problemas:

• encontrar un punto de corte» óptimo » puede ser muy dependiente del conjunto de datos e imposible de replicar en diferentes estudios. Además, al hacer comparaciones múltiples, corremos el riesgo de aumentar las posibilidades de falsos positivos (encontrar una diferencia en las funciones de supervivencia, cuando en realidad no hay ninguna).
• La Dicotomización disminuye el poder de la prueba estadística forzando todas las mediciones a un valor binario, lo que a su vez puede llevar a la necesidad de un tamaño de muestra mucho mayor requerido para detectar un efecto., También vale la pena mencionar que con el análisis de supervivencia, el tamaño de muestra requerido se refiere al número de observaciones con el evento de interés.
• Al dicotomizar, hacemos malas suposiciones sobre la distribución del riesgo entre las observaciones. Supongamos que usamos la edad de 50 como la división entre pacientes jóvenes y ancianos. Si lo hacemos, asumimos que un niño de 18 años está en el mismo grupo de riesgo que un niño de 49 años, lo que no es cierto en la mayoría de los casos.,

Teniendo en cuenta solo un predictor

el estimador de Kaplan-Meier es un método univariable, ya que se aproxima a la función de supervivencia utilizando como máximo una variable/predictor. Como resultado, los resultados pueden ser fácilmente sesgados, ya sea exagerando o perdiendo la señal. Esto es causado por el llamado sesgo de variable omitida, que hace que el análisis asuma que los efectos potenciales de múltiples predictores deben atribuirse solo al único, que tenemos en cuenta. Debido a eso, se deben usar métodos multivariables como la regresión de Cox.,

ejemplo en Python

Es hora de implementar lo que hemos aprendido en la práctica. Comenzamos importando todas las bibliotecas requeridas.

luego, cargamos el conjunto de datos y hacemos un pequeño forcejeo para que funcione bien con la biblioteca lifelines. Para el análisis, utilizamos el popular conjunto de datos de cancelación de clientes de Telco (disponible aquí o en mi GitHub)., El conjunto de Datos contiene información del cliente de un proveedor de teléfono / internet, incluida su tenencia, qué tipo de servicios utilizan, algunos datos demográficos y, en última instancia, la bandera que indica la pérdida.,

Para este análisis, utilizamos las siguientes columnas:

• tenure — el número de meses que el cliente se ha quedado con la empresa,
• churn información si el cliente se agitaba (binario codificado: 1 si el evento ocurrió, 0 en caso contrario),
• PaymentMethod— ¿qué tipo de método de pago de los clientes que utilizan.,

para el escenario más básico, en realidad solo necesitamos el time-to-event y la bandera que indica si ocurrió el evento de interés.

El KaplanMeierFitter funciona de manera similar a las clases conocidas de scikit-learn: primero hablamos de crear una instancia del objeto de la clase y, a continuación, utilizar la etiqueta fit método para ajustar el modelo a los datos., Durante el trazado, especificamos at_risk_counts=True para mostrar adicionalmente información sobre el número de observaciones en riesgo en ciertos momentos.

Normalmente, estaríamos interesados en la mediana del tiempo de supervivencia, es decir, el punto en el tiempo en el que en promedio el 50% de la población ha muerto ya, o en este caso, se agitaba., Podemos acceder a él usando la siguiente línea:

kmf.median_survival_time_

Sin embargo, en este caso, el comando devuelve inf, como podemos ver en la curva de supervivencia que en realidad no observamos ese punto en nuestros datos.

hemos visto el caso de uso básico, ahora vamos a complicar el análisis y trazar las curvas de supervivencia para cada variante del método de pago., Podemos hacerlo ejecutando el código siguiente:

se Ejecuta el bloque de código se genera el siguiente diagrama:

Podemos ver que la probabilidad de supervivencia es sin duda la más baja de la electrónica de cheques, mientras que las curvas de una transferencia bancaria/tarjeta de crédito son muy similares., Este es el momento perfecto para usar la prueba de rango logarítmico para ver si son realmente diferentes.

La siguiente tabla se presentan los resultados.

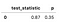
mirando el p-valor de 0,35, podemos ver que no hay razones para rechazar la hipótesis nula que indica que la supervivencia de las funciones son idénticas. Para este ejemplo, solo comparamos dos métodos de pago., Sin embargo, definitivamente hay más combinaciones que podríamos probar. Hay una práctica función llamada pairwise_logrank_test , que hace que la comparación sea muy fácil.

En la tabla, podemos ver la comparativa que hicimos, así como de todas las otras combinaciones. La transferencia bancaria vs, la tarjeta de crédito es el único caso en el que no debemos rechazar la hipótesis nula. Además, debemos ser cautelosos al interpretar los resultados de la prueba log-rank, como podemos ver en la gráfica anterior que las curvas para los pagos por transferencia bancaria y tarjeta de crédito realmente se cruzan, por lo que se viola el supuesto de riesgos proporcionales.

Hay dos cosas más que podemos probar fácilmente usando la biblioteca lifelines. La primera es la prueba de log-rank multivariante, en la que la hipótesis nula establece que todos los grupos tienen el mismo proceso de generación de «muerte», por lo que sus curvas de supervivencia son idénticas.,

Los resultados de la prueba indican que debemos rechazar la hipótesis nula, por lo que las curvas de supervivencia no son idénticos, lo que ya hemos visto en la trama.

Por último, podemos probar la diferencia de supervivencia en un punto específico en el tiempo. Volviendo al ejemplo, en la gráfica, podemos ver que las curvas están más separadas alrededor de t = 60., Veamos si esa diferencia es estadísticamente significativa.

mirando la prueba de la p-valor, no hay ninguna razón para rechazar la hipótesis nula que indica que no hay ninguna diferencia entre la supervivencia en ese punto del tiempo.

conclusiones

en este artículo, describí una herramienta muy popular para realizar análisis de supervivencia: el estimador de Kaplan — Meier., También cubrimos la prueba de rango logarítmico para comparar dos / múltiples funciones de supervivencia. El enfoque descrito es muy popular, sin embargo, no sin defectos. Antes de concluir, echemos un vistazo a los pros y los contras del estimador/curvas de Kaplan-Meier.

ventajas:

• proporciona la visión media de la población, también por grupos.
• No requiere muchas características, solo la información sobre la hora de Evento y si el evento realmente ocurrió. Además, podemos usar cualquier característica categórica que describa grupos.,
• automáticamente maneja el desequilibrio de clase, ya que prácticamente cualquier proporción de muerte a eventos censurados es aceptable.
• Como es un método no paramétrico, se hacen pocas suposiciones sobre la distribución subyacente de los datos.

desventajas:

• no podemos evaluar la magnitud del impacto del predictor en la probabilidad de supervivencia.
• no podemos tener en cuenta simultáneamente múltiples factores para las observaciones, por ejemplo, el país de origen y el sistema operativo del teléfono.,
• El supuesto de independencia entre la censura y la supervivencia (en el momento t, Las observaciones censuradas deben tener el mismo pronóstico que las que no censuran) puede ser inaplicable/poco realista.
• Cuando la distribución de datos subyacente es (hasta cierto punto) conocida, el enfoque no es tan preciso como algunas técnicas competidoras.

resumiendo, incluso con algunas desventajas, las curvas de supervivencia de Kaplan-Meier son un excelente lugar para comenzar mientras se realizan análisis de supervivencia., Al hacerlo, podemos obtener información valiosa sobre los predictores potenciales de supervivencia y acelerar nuestro progreso con algunas técnicas más avanzadas (que describiré en futuros artículos).

puedes encontrar el código utilizado para este artículo en mi GitHub. Como siempre, cualquier comentario constructivo es bienvenido. Puedes contactarme en Twitter o en los comentarios.

en caso de que te interese este artículo, también te gustarán los otros de la serie:

S. Sawyer (2003)., Los intervalos de confianza de Greenwood y Greenwood exponencial en el análisis de supervivencia-disponible aquí

curvas de supervivencia de Kaplan-Meier y la prueba de rango Log — disponible aquí

peligros no proporcionales-¿y qué? — disponible aquí

Bouliotis, G., & Billingham, L. (2011). Cruce de curvas de supervivencia: alternativas a la prueba de rango logarítmico. Trials, 12 (S1), A137.