resolver ecuaciones polinómicas de orden superior es una habilidad esencial para cualquiera que estudie ciencias y matemáticas. Sin embargo, entender cómo resolver este tipo de ecuaciones es bastante desafiante.
en este artículo, vamos a aprender cómo resolver las ecuaciones cúbicas utilizando diferentes métodos como el método de división, el teorema del Factor y la factorización por agrupación.
pero antes de entrar en este tema, vamos a discutir lo que es un polinomio y ecuación cúbica.,
un polinomio es una expresión algebraica con uno o más Términos en los que una constante y una variable están separadas por un signo de suma o resta.
La forma general de un polinomio es axn + bxn-1 + cxn-2 + …. + kx + l, donde cada variable tiene una constante que la acompaña como su coeficiente. Los diferentes tipos de polinomios incluyen; binomios, trinomios y cuadrinomios. Ejemplos de polinomios son; 3x + 1, x2 + 5xy – ax – 2ay, 6×2 + 3x + 2x + 1 etc.
una ecuación cúbica es una ecuación algebraica de tercer grado.,la forma general de una función cúbica es: f (x) = ax3 + bx2 + cx1 + d. y la ecuación cúbica tiene la forma de ax3 + bx2 + cx + d = 0, donde A, b y c son los coeficientes y d es la constante.
Cómo Resolver Ecuaciones Cúbicas?
la forma tradicional de resolver una ecuación cúbica es reducirla a una ecuación cuadrática y luego resolverla mediante factorización o fórmula cuadrática.
Como una ecuación cuadrática tiene dos raíces reales, una ecuación cúbica puede tener, posiblemente, tres raíces reales., Pero a diferencia de la ecuación cuadrática que puede no tener ninguna solución real, una ecuación cúbica tiene al menos una raíz real.
las otras dos raíces pueden ser reales o imaginarias.
cada vez que se te da una ecuación cúbica, o cualquier ecuación, siempre tienes que organizarla en una forma estándar primero.
por ejemplo, si se le da algo como esto, 3×2 + x-3 = 2/x, se reorganizará en el formulario estándar y lo escribirá como, 3×3 + x2-3x – 2 = 0. Entonces usted puede resolver esto por cualquier método adecuado.,
veamos algunos ejemplos a continuación para una mejor comprensión:
Ejemplo 1
determinar las raíces de la ecuación cúbica 2×3 + 3×2 – 11x – 6 = 0
solución
ya que d = 6, Entonces los factores posibles son 1, 2, 3 y 6.
Ahora aplique el teorema del Factor para verificar los posibles valores por ensayo y error.
f (1) = 2 + 3 – 11 – 6 ≠ 0
f (-1) = -2 + 3 + 11 – 6 ≠ 0
f (2) = 16 + 12 – 22 – 6 = 0
por lo tanto, x = 2 es la primera raíz.
por lo Tanto, las soluciones son x = 2, x = -1/2 y x = -3.,
Ejemplo 2
Encontrar las raíces de la ecuación cúbica x3 − 6×2 + 11x – 6 = 0
Solución
x3 − 6×2 + 11x – 6
(x – 1) es uno de los factores.
Al dividir x3 − 6×2 + 11x – 6 (x – 1),
⟹ (x – 1) (x2 – 5x + 6) = 0
⟹ (x – 1) (x – 2) (x – 3) = 0
Este de la cúbico soluciones de la ecuación son x = 1, x = 2 y x = 3.
Ejemplo 3
Resolver x3 – 2×2 – x + 2
Solución
Factorizar la ecuación.
x3 – 2×2 – x + 2 = x2(x – 2) – (x – 2)
= (x2 – 1) (x – 2)
= (x + 1) (x – 1) (x – 2)
x = 1, -1 y 2.,
Example 4
Solve the cubic equation x3 – 23×2 + 142x – 120
Solution
First factorize the polynomial.
x3 – 23×2 + 142x – 120 = (x – 1) (x2 – 22x + 120)
But x2 – 22x + 120 = x2 – 12x – 10x + 120
= x (x – 12) – 10(x – 12)
= (x – 12) (x – 10)
Therefore, x3 – 23×2 + 142x – 120 = (x – 1) (x – 10) (x – 12)
Equate each factor to zero.
x – 1= 0
x = 1
x – 10 = 10
x – 12= 0
x = 12
The roots of the equation are x = 1, 10 and 12.
Example 5
Solve the cubic equation x3 – 6 x2 + 11x – 6 = 0.,
solución
para resolver este problema usando el método de división, tome cualquier factor de la constante 6;
deje que x = 2
divida el polinomio por x-2 a
(x2 – 4x + 3) = 0.
ahora resuelve la ecuación cuadrática (x2-4x + 3)= 0 para obtener x = 1 o x = 3
Por lo tanto, las soluciones son x= 2, x =1 y x = 3.
Ejemplo 6
resolver la ecuación cúbica x3 – 7×2 + 4x + 12 = 0
solución
Let f(x) = x3 – 7×2 + 4x + 12
dado que d = 12, los valores posibles son 1, 2, 3, 4, 6 y 12.,
por ensayo y error, encontramos que f (-1) = -1 – 7 – 4 + 12 = 0
así, (x + 1) es un factor de la función.
x3 – 7×2 + 4x + 12
= (x + 1) (x2 – 8x + 12)
= (x + 1) (x – 2) (x – 6)
por lo Tanto, x = -1, 2, 6
Ejemplo 7
Resolver la siguiente ecuación cúbica:
x3 + 3×2 + x + 3 = 0.
Solución
x3 + 3×2 + x + 3
= (x3 + 3×2) + (x + 3)
= x2(x + 3) + 1(x + 3)
= (x + 3) (x2 + 1)
por lo Tanto, x = -1 ,1 -3.,
Example 8
Solve x3 − 6×2 + 11x − 6 = 0
Solution
Factorize
x3 − 6×2 + 11x − 6 = 0 ⟹ (x − 1) (x − 2) (x − 3) = 0
Equating each factor to zero gives;
x = 1, x = 2 and x = 3
Example 9
Solve x 3 − 4×2 − 9x + 36 = 0
Solution
Factorize each set of two terms.,ing de cada factor a cero, obtenemos;
x = -3, 3 o 4
Ejemplo 10
Resolver la ecuación 3×3 −16×2 + 23x − 6 = 0
Solución
Divida 3×3 −16×2 + 23x – 6 x -2 para obtener 3×2 – 1x – 9x + 3
= x (3x – 1) – 3(3x – 1)
= (x – 3) (3x – 1)
por lo Tanto, 3×3 −16×2 + 23x − 6 = (x – 2) (x – 3) (3x – 1)
Igualar cada factor a cero para obtener,
x = 2, 3 y 1/3
Ejemplo 11
Encontrar las raíces de 3×3 – 3×2 – 90x=0
Solución
factor a cabo 3x
3×3 – 3×2 – 90x ⟹3x (x2 – x – 30)
Encontrar un par de factores cuyo producto es de -30 y la suma es -1.,
⟹- 6 * 5 =-30
⟹ -6 + 5 = -1
escribir la ecuación sustituyendo el término «bx» con el elegido factores.
Factor 3x
Factor de la ecuación;
⟹ 3x
= 3x (x – 6) (x + 5)
equiparando cada factor a cero, obtenemos;
x = 0, 6, -5
resolviendo ecuaciones cúbicas usando el método gráfico
Si no puede resolver la ecuación cúbica por cualquiera de los métodos anteriores, puede resolverla gráficamente. Para eso, necesita tener un boceto preciso de la ecuación cúbica dada.,
el punto(s) donde su grafo cruza el eje x, es una solución de la ecuación. El número de soluciones reales de las ecuaciones cúbicas es el mismo que el número de veces que su gráfico cruza el eje X.
Ejemplo 12
Encuentra las raíces de x3 + 5×2 + 2x – 8 = 0 gráficamente.
Solución
Simplemente dibujar la gráfica de la siguiente función sustituyendo valores aleatorios de x:
f (x) = x3 + 5×2 + 2x – 8
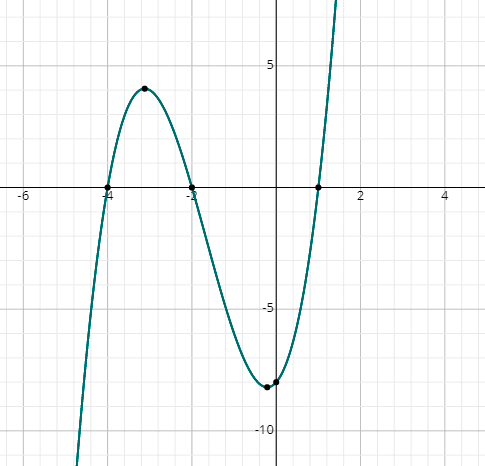
Se puede ver la gráfica corta el eje x en 3 puntos, por lo tanto, hay 3 soluciones reales.,
en el gráfico, las soluciones son:
x = 1, x = -2 & x = -4.
Preguntas de Práctica
Resolver las siguientes ecuaciones cúbicas: