la Géométrie Non-Euclidienne

le postulat parallèle

Le Cinquième postulat dans les éléments D’Euclide peut être reformulé comme

Le postulat n’est pas vrai en 3D, mais en 2D, il semble être une instruction valide., Considérant l’importance des postulatscependant, une déclaration apparemment valide n’est pas assez bonne.

Un postulat (ou axiome) est un énoncé qui sert de point de départ pour une théorie. Comme un postulat est un point de départ, il ne peut pas être prouvé en utilisant le résultat précédent. En tant que Déclaration qui ne peut être prouvée, un postulat devrait aller de soi. Les Éléments d’Euclide est construit sur cinq postulats., Pendant plus de 2000 ans, le cinquième postulat a été considéré comme moins intuitif que les autres postulats, et pas suffisamment évident. De nombreuses tentatives ont été faites pour prouver le cinquième postulat en utilisant les quatre autres postulats. Toutes ces tentatives ont échoué. Au 19e siècle, il a été montré que le cinquième postulat est indépendant des autres postulats. Il est possible de construire une théorie de la géométrie où le cinquième postulat n’est pas vrai. De telles géométries sont appelées non euclidiennes. De plus, on peut montrer que les théories non euclidiennes peuvent être aussi cohérentes que la théorie euclidienne., Une théorie est cohérente si elle ne contient aucune contradiction.

l’énoncé inverse au postulat parallèle, comme indiqué ci-dessus, est qu’il n’y a pas de lignes, ou au moins deux lignes « parallèles à la ligne donnée à travers le point ». On peut montrer que s’il y a au moins deux lignes, il y a en fait infiniment de lignes « parallèles à… ».

si le postulat parallèle est remplacé par:

vous obtenez une géométrie elliptique.,

si le postulat parallèle est remplacé par:

vous obtenez une géométrie hyperbolique.

Distances, angles et lignes

Les théorèmes dans les Éléments d’Euclide sont construites sur un certain nombre de postulats et d’un certain nombre de définitions. La définition numéro 23 indique que deux lignes sont parallèles si elles ne se rencontrent jamais., Rien dans la définition n’indique que la distance entre deux lignes parallèles est la même partout. Le postulat parallèle n’est apparemment évident que si vous supposez que les lignes parallèles ressemblent à des voies ferrées. Si vous redéfinissez ce que vous entendez par une ligne, vous pouvez avoir que deux lignes parallèles convergent l’une vers l’autre ou divergent l’une de l’autre.

en géométrie non euclidienne, le concept correspondant à une droite est une courbe appelée géodésique. En géométrie non euclidienne, un chemin le plus court entre deux points est le long d’une telle géodésique, ou « ligne non euclidienne ».,

Tous les théorèmes de la géométrie euclidienne qui utilisent le cinquième postulat seront modifiés lorsque vous reformulerez le postulat parallèle. A titre d’exemple; en géométrie euclidienne la somme des angles intérieurs d’un triangle est de 180°, en géométrie non euclidienne ce n’est pas le cas.

Modèle de géométrie elliptique

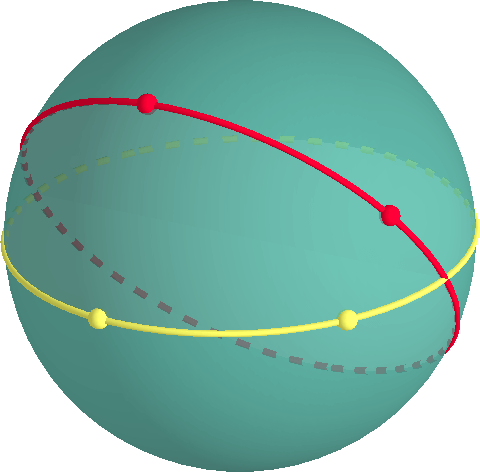
Un moyen facile de le modèle elliptique de la géométrie est de considérer la géométrie de la surface d’une sphère. Un chemin le plus court entre deux points sur l’asphère est le long d’un soi-disant grand cercle., Un grand cercle est un cercle de même rayon, et le même centre que la sphère. Un grand cercle est une géodésique.

Si deux points sont directement opposés sur la sphère (comme le pôle Nord et le pôle Sud), il y a infiniment de chemins Les plus courts entre les points. Si les points ne sont pasantipodes, il n’y a qu’un seul chemin le plus court.

Deux grands cercles qui ne sont pas les mêmes, doivent se croisent. Par conséquent, il n’y a pas de lignes parallèles à la surface d’une sphère.

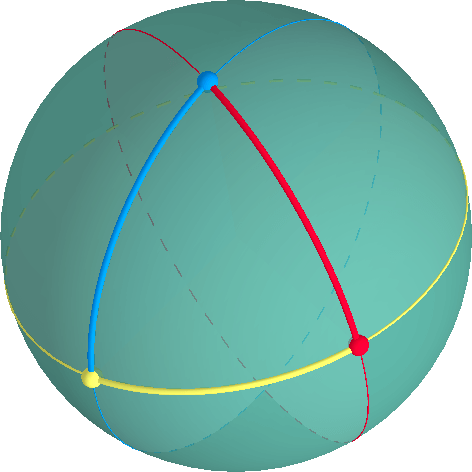
un triangle est défini par trois sommets et trois arcs le long de grands cercles à travers chaque paire de Sommets.,

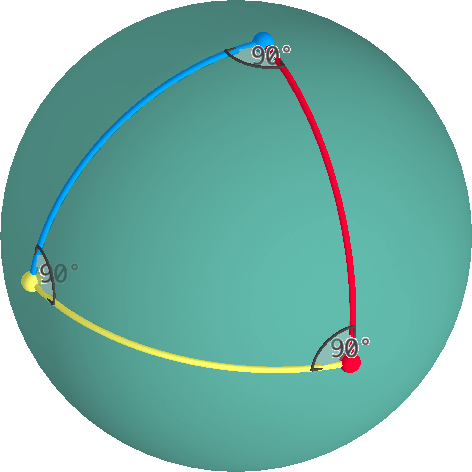
Un angle intérieur à l’un des sommets d’un triangle peut être mesurée sur le plan tangent à travers ce sommet. La somme des angles intérieurs d’un triangle elliptique est toujours > 180°.

géométrie hyperbolique utilisant le modèle de disque de Poincaré

Le disque de Poincaré (en 2D) est un disque ouvert, c’est-à-dire un ensemble de points délimités par un cercle n’incluant pas le cercle., Lors de l’utilisation du modèle de disque Poincaré, seuls les points du disque Poincaré sont pris en compte. Le disque Poincaré fait le monde entier. La limite du disque ouvert est le cercle à l’infini, \(C_ \ infty \).

un angle intérieur d’un triangle est mesuré entre les lignes tangentes correspondantes., La somme des angles intérieurs est toujours < 180°. Si les sommets d’un triangle se déplacent vers le cercle \(C_\infty \), la somme des angles tend vers 0. Les Points qui se trouvent à \(C_ \ infty \) sont appelés points idéaux. Le triangle de limitation comme les sommets tendent à l’infini (\(C_ \ infty \)) est appelé un triangle idéal. Un triangle idéal a une somme d’angle 0. Depuis les sommets d’un triangle idéal allonger à l’infini, le périmètre d’un triangle idéal est infini. De plus, on peut montrer que l’aire d’un triangle idéal est \(\pi\)., Par conséquent, tous les triangles de l’animation la plus haute ont la même zone hyperbolique.

géométrie hyperbolique utilisant le modèle de demi-plan de Poincaré

Une ligne divise un plan en deux moitiés. Lors de l’utilisation du modèle de demi-plan Poincaré, seuls les points dans la moitié d’un plan (sans compter la ligne) sont pris en compte.

exercices

Exercice 1

pour les géométries non euclidiennes, tous les postulats des éléments D’Euclide, à l’exception du postulat parallèle, doivent être vrais. Si vous utilisez la géométrie sur une sphère pour modéliser la géométrie elliptique, ce n’est pas le cas (selon la façon dont vous interprétez le premier postulat). Utilisez le Guide pour le postulat 1 pour expliquer pourquoi la géométrie sur une sphère, comme expliqué dans le texte, n’est pas strictement non euclidienne.

Exercice 2

logiciel geogebra a la construction de l’elliptique géodésique.

utilisation de GeoGebra afficher la fenêtre graphique 3D!, Vous pouvez créer des sphères et des plans en utilisant des commandes ou des outils. Pour utiliser une commande, commencez à taper Sphere (ou Plane) et GeoGebra vous montrera diverses alternatives pour compléter le code.

un cercle sur une sphère peut être construit en coupant la sphère avec un plan. Vous faites une intersection à l’aide de L’outil Intersect Two Surfaces. Un grand cercle est construit en choisissant un plan approprié pour croiser la sphère avec.,

Exercice 3

Mesurer un angle entre deux géodésiques sur une sphère à l’aide de logiciel geogebra a.

placez trois points \(A\), \(B\) et \(C\) sur une sphère et construisez deux géodésiques qui forment l’angle elliptique \( \angle ABC \). L’angle est mesuré en utilisant des points sur le plan passant par \(B\) tangent à la sphère. Construire le plan tangent. Construisez deux points sur le plan qui peuvent être utilisés pour mesurer l’angle. Mesurez l’angle et cachez tous les objets auxiliaires.,

animated gifs:

Ideal triangles on Ello.