Introducere
Introducere
La postulatul
Cel de-al cincilea postulat în Elementele lui Euclid poate fi reformulată ca
postulatul nu este adevărat în 3D, dar în 2D pare a fi o declarație validă., Având în vedere importanța postulatelorcu toate acestea, o declarație aparent valabilă nu este suficient de bună.

Un postulat (sau axioma) este o declarație care acționează ca un punct de plecare pentru o teorie. Deoarece un postulat este un punct de plecare, nu poate fi dovedit folosind rezultatul anterior. Ca o afirmație care nu poate fi dovedită, un postulat ar trebui să fie evident. Elementele lui Euclid sunt construite pe cinci postulate., De peste 2000 de ani, cel de-al cincilea postulat a fost considerat a fi mai puțin intuitiv decât celelalte postulate și nu suficient de evident. Au fost făcute multe încercări de a dovedi al cincilea postulat folosind celelalte patru postulate. Toate aceste încercări au eșuat. În secolul al XIX-lea sa arătat că al cincilea postulat este independent de celelalte postulate. Este posibil să se construiască o teorie a geometriei în care al cincilea postulat nu este adevărat. Astfel de geometrii sunt numite non-euclidiene. În plus, se poate demonstra că teoriile non-euclidiene pot fi la fel de consistente ca teoria euclidiană., O teorieeste consecventă dacă nu conține nicio contradicție.
declarația inversă a postulatului paralel, așa cum sa menționat mai sus, este că nu există linii sau cel puțin două linii „paralele cu linia dată prin punct”. Se poate arăta că, dacă există cel puțin două linii, există, de fapt, infinit de multe linii „paralele cu…”.
dacă postulatul paralel este înlocuit cu:
obțineți o geometrie eliptică.,dacă postulatul paralel este înlocuit cu:
obțineți o geometrie hiperbolică.
Distanțe, unghiuri și linii

teoreme în Elementele de Euclid sunt construite pe o serie de postulate și o serie de definiții. Definiția numărul 23 afirmă că două linii sunt paralele dacă nu se întâlnesc niciodată., Nu există nimic în definiție care să indice că distanța dintre două linii paralele este aceeași peste tot. Postulatul paralel este aparent evident numai dacă presupunem că liniile paralele arată ca niște căi ferate. Dacă redefiniți ceea ce înțelegeți printr-o linie, este posibil să aveți că două linii paralele fie converg una spre cealaltă, fie se deosebesc una de cealaltă.
în geometria non-euclidiană, conceptul corespunzător unei linii este o curbă numită geodezică. În geometria non-euclidiană, o cale cea mai scurtă între două puncte este de-a lungul unei astfel de linii geodezice sau „non-euclidiene”.,
toate teoremele din geometria euclidiană care utilizează al cincilea postulat, vor fi modificate atunci când reformulați postulatul paralel. Ca exemplu; în geometria euclidiană suma unghiurilor interioare ale unui triunghi este de 180°, în geometria non-euclidiană nu este cazul.
Model de eliptice geometrie
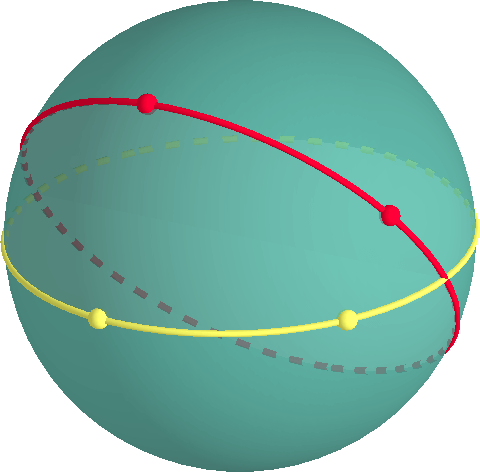
O modalitate ușoară de a modelul geometrie eliptică este să ia în considerare geometria pe suprafața unei sfere. O cale cea mai scurtă între două puncte pe asphere este de-a lungul unui așa-numit cerc mare., Un cerc mare este un cerc având aceeași rază, și același centru, ca sfera. Un cerc mare este un geodezic. dacă două puncte sunt direct opuse unul față de celălalt pe sferă (cum ar fi Polul Nord și Polul Sud), există infinit de multe căi cele mai scurte între puncte. Dacă punctele nu suntantipode, există o singură cale cea mai scurtă.
două cercuri mari care nu sunt aceleași, trebuie să se intersecteze. Prin urmare, nu există linii paralele pe suprafața unei sfere.un triunghi este definit de trei vârfuri și trei arce de-a lungul cercurilor mari prin fiecare pereche de vârfuri.,
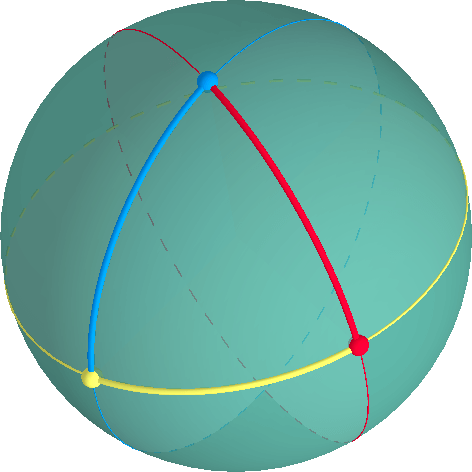
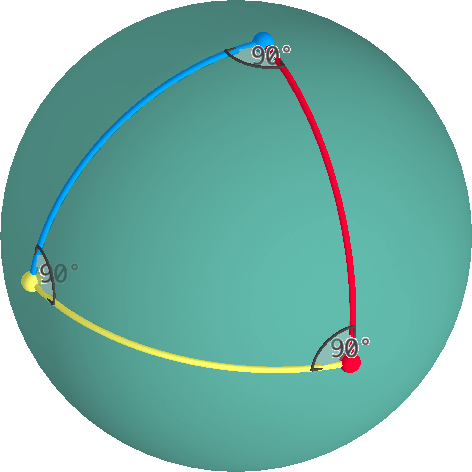
Un unghi interior de la un vârf al unui triunghi poate fi măsurată pe plan tangent prin acest nod. Suma unghiurilor interioare ale unui triunghi eliptic este întotdeauna > 180°.
geometrie Hiperbolica folosind Poincaré disc model
Poincaré disc (în 2D) este un open disc, adică un set de puncte delimitată de un cerc nu, inclusiv cerc., Când utilizați modelul discului Poincaré, sunt luate în considerare numai punctele din discul Poincaré. Discul Poincaré alcătuiește întreaga lume. Limita discului deschis este cercul la infinit, \(C_\infty \).

având în vedere un geodezic alb și un punct alb care nu este pe el, există infinit de multe geodezice
prin punctul alb care nu intersectează geodezicul alb.
un unghi interior al unui triunghi este măsurat între liniile tangente corespunzătoare., Suma unghiurilor interioare este întotdeauna < 180°. Dacă vârfurile unui triunghi se deplasează spre cercul \(C_\infty \), suma unghiului tinde la 0. Punctele care se află la \(C_ \ infty \) se numesc puncte ideale. Triunghiul limitativ, deoarece vârfurile tind spre infinit (\(C_ \ infty \)) se numește triunghi ideal. Un triunghi ideal are suma unghiului 0. Deoarece vârfurile unui triunghi ideal se află la infinit, perimetrul unui triunghi ideal este infinit. În plus, se poate demonstra că aria unui triunghi ideal este \(\pi\)., Prin urmare, toate triunghiurile din animația de sus au aceeași zonă hiperbolică.

geometrie Hiperbolica folosind Poincaré halfplane model
O linie împarte un avion în două jumătăți. Atunci când se utilizează modelul Poincaré halfplane, sunt luate în considerare numai punctele din jumătate de plan (fără a include linia).

Exerciții
Exercitiul 1
Pentru non-Euclidiană geometrii toate postulatele în Elementele lui Euclid, cu excepția postulatul ar trebui să fie adevărat. Dacă utilizați geometria pe o sferă pentru a modela geometria eliptică, acest lucru nu este cazul (în funcție de modul în care interpretați primul postulat). Utilizați Ghidul pentru postulatul 1 pentru a explica de ce geometria pe o sferă, așa cum este explicat în text, nu este strict non-euclidiană.
Exercițiul 2
GeoGebra construcția geodezică eliptică.
folosind GeoGebra Arată fereastra grafică 3D!, Puteți face sfere și avioane folosind comenzi sau instrumente. Pentru a utiliza o comandă începeți să tastați Sphere (sau Plane) și GeoGebra vă va arăta diferite alternative pentru completarea codului.un cerc pe o sferă poate fi construit prin intersectarea sferei cu un plan. Faceți o intersecție utilizând instrumentul intersectați două suprafețe. Un cerc mare este construit prin alegerea unui plan adecvat pentru a intersecta sfera cu.,
3
Măsura un unghi între două geodezice pe o sferă folosind GeoGebra.
puneți trei puncte \(A\), \(B\) și \(C\) pe o sferă și construiți două geodezice care formează unghiul eliptic \( \angle ABC \). Unghiul este măsurat prin utilizarea punctelor de pe plan prin\ (B\) tangentă la sferă. Construiți planul tangent. Construiți două puncte pe plan care pot fi utilizate pentru a măsura unghiul. Măsurați unghiul și ascundeți toate obiectele auxiliare.,
animated gifs:
Ideal triangles on Ello.