Geometría No-Euclidiana

el postulado paralelo

El quinto postulado en los elementos de Euclides se puede reformular como

el postulado no es verdadero en 3D pero en 2D parece ser una declaración válida., Teniendo en cuenta la importancia de postulateshowever, una declaración aparentemente válida no es suficiente.

un postulado (o axioma) es una declaración que actúa como punto de partida para una teoría. Dado que un postulado es un punto de partida, no se puede probar usando un resultado anterior. Como una afirmación que no puede ser probada, un postulado debe ser evidente por sí mismo. Los elementos de Euclides se basa en cinco postulados., Por más de 2000 años el quinto postulado ha sido considerado menos intuitivo que los otros postulados, y no suficientemente evidente. Se han hecho muchos intentos para probar el quinto postulado usando los otros cuatro postulados. Todos estos intentos han fracasado. En el siglo XIX se demostró que el quinto postulado es independiente de los otros postulados. Es posible construir una teoría de la geometría donde el quinto postulado no es cierto. Tales geometrías se llaman no euclidianas. Además, se puede demostrar que las teorías no euclidianas pueden ser tan consistentes como la teoría euclidiana., Una teoría es consistente si no contiene ninguna contradicción.

la declaración inversa al postulado paralelo, como se indicó anteriormente, es que no hay líneas, o al menos dos líneas «paralelas a la línea dada a través del punto». Se puede demostrar que si hay al menos dos líneas, hay de hecho infinitamente muchas líneas «paralelas a…».

si el postulado paralelo es reemplazado por:

se obtiene una geometría elíptica.,

si el postulado paralelo es reemplazado por:

se obtiene una geometría hiperbólica.

distancias, ángulos y líneas

Los teoremas en los elementos de Euclides se basan en una serie de postulados y una serie de definiciones. La definición número 23 establece que dos rectas son paralelas si nunca se encuentran., No hay nada en la definición que indique que la distancia entre dos líneas paralelas es la misma en todas partes. El postulado paralelo es aparentemente obvio solo si asumes que las líneas paralelas se parecen a las vías del ferrocarril. Si se redefine lo que se entiende por una línea, es posible que dos líneas paralelas converjan una hacia la otra o diverjan una de la otra.

en Geometría no euclidiana, el concepto correspondiente a una recta es una curva llamada geodésica. En Geometría no euclidiana un camino más corto entre dos puntos es a lo largo de tal geodésica, o «línea no euclidiana».,

Todos los teoremas en geometría euclidiana que utilizan el quinto postulado, se alterarán cuando se reformule el postulado paralelo. Como ejemplo, en geometría euclidiana la suma de los ángulos interiores de un triángulo es de 180°, en Geometría no euclidiana este no es el caso.

Modelo de geometría elíptica

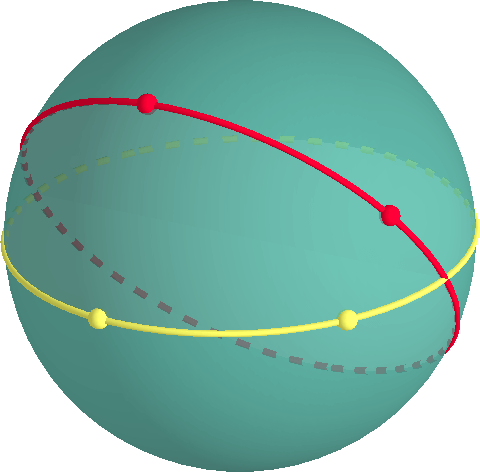
Una forma fácil para modelar la geometría elíptica es considerar la geometría de la superficie de una esfera. Un camino más corto entre dos puntos en asphere es a lo largo de un llamado Gran Círculo., Un gran círculo es un círculo que tiene el mismo radio y el mismo centro que la esfera. Un gran círculo es una geodésica.

si dos puntos están directamente opuestos entre sí en la esfera (como el polo norte y el polo sur) hay infinitos caminos más cortos entre los puntos. Si los puntos no son antípodos, solo hay un camino más corto.

dos grandes círculos que no son lo mismo, deben intersectarse. Por lo tanto, no hay líneas paralelas en la superficie de una esfera.

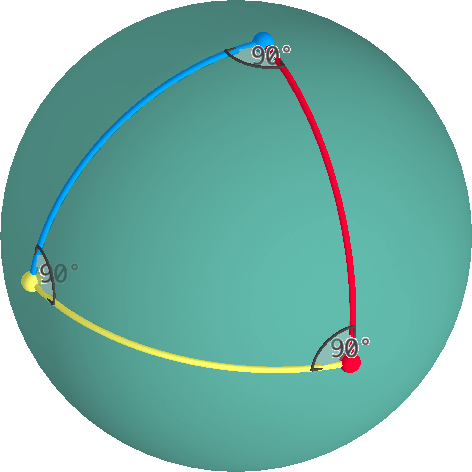
un triángulo está definido por tres vértices y tres arcos a lo largo de grandes círculos a través de cada par de vértices.,

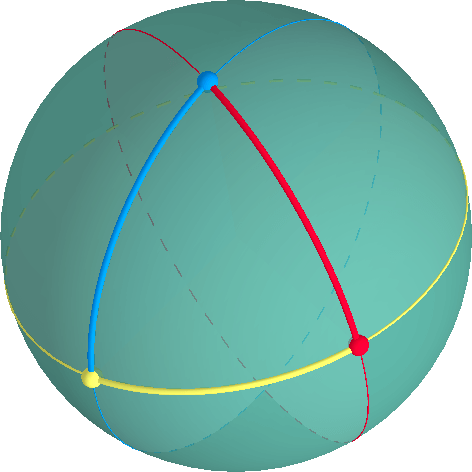
Un ángulo interior en un vértice de un triángulo puede ser medido en el plano tangente a través de ese vértice. La suma de los ángulos interiores de un triángulo elíptico es siempre > 180°.

geometría hiperbólica utilizando el modelo de disco Poincaré

El disco Poincaré (en 2D) es un disco abierto, es decir, un conjunto de puntos delimitados por un círculo que no incluye círculo., Cuando se utiliza el modelo de disco de Poincaré, solo se consideran los puntos en el disco de Poincaré. El disco de Poincaré constituye el mundo entero. El límite del disco abierto es el círculo en el infinito, \(C_ \ infty \).

un ángulo interior de un triángulo se mide entre las líneas tangentes correspondientes., La suma de los ángulos interiores es siempre < 180°. Si los vértices de un triángulo se mueven hacia el círculo \(C_ \ infty \), la suma del ángulo tiende a 0. Los puntos que se encuentran en \(C_\infty \) se denominan puntos ideales. El triángulo limitante como los vértices tienden al infinito (\(C_\infty \)) se llama un triángulo ideal. Un triángulo ideal tiene suma de ángulo 0. Dado que los vértices de un triángulo ideal se encuentran en el infinito, el perímetro de un triángulo ideal es infinito. Además, se puede demostrar que el área de un triángulo ideal es \(\pi\)., Por lo tanto, todos los triángulos en la animación superior tienen la misma área hiperbólica.

geometría hiperbólica usando el modelo de semiplano de Poincaré

Una Línea divide un plano en dos mitades. Cuando se utiliza el modelo de semiplano de Poincaré, solo se consideran los puntos en la mitad de un plano (sin incluir la línea).

ejercicios

Ejercicio 1

para geometrías no euclidianas todos los postulados en los elementos de Euclides excepto el postulado paralelo deben ser verdaderos. Si usa geometría en una esfera para modelar Geometría elíptica, este no es el caso (dependiendo de cómo interprete el primer postulado). Use la Guía del postulado 1 para explicar por qué la geometría en una esfera, como se explica en el texto, no es estrictamente no euclidiana.

Ejercicio 2

GeoGebra construcción de elíptica geodésica.

Usando GeoGebra mostrar la ventana de gráficos 3D!, Puedes hacer esferas y planos usando comandos o herramientas. Para usar un comando, comience a escribir Sphere(o Plane) y GeoGebra le mostrará varias alternativas para completar el código.

un círculo en una esfera se puede construir intersectando la esfera con un plano. Puede hacer una intersección utilizando la herramienta Intersecar dos superficies. Un gran círculo se construye eligiendo un plano apropiado para intersectar la esfera con.,

Ejercicio 3

Medir el ángulo entre dos geodesics en una esfera utilizando GeoGebra.

ponga tres puntos \(A\), \(B\) y \(C\) En una esfera y construya dos geodésicas que forman el ángulo elíptico \ (\angle ABC \). El ángulo se mide usando puntos en el plano a través de\ (B\) tangente a la esfera. Construir el plano tangente. Construir dos puntos en el plano que se pueden utilizar para medir el ángulo. Mida el ángulo y oculte todos los objetos auxiliares.,

animated gifs:

Ideal triangles on Ello.