Introdução
Introdução
O paralelo postulado
O quinto postulado de Euclides Elementos pode ser reformulada como:
o postulado não é verdadeiro em 3D, mas em 2D parece ser uma afirmação válida., Considerando a importância do postulateshowever, uma declaração aparentemente válida não é suficiente.

um postulado (ou axioma) é uma afirmação que atua como um ponto de partida para uma teoria. Uma vez que um postulado é um ponto de partida, não pode ser provado usando o resultado anterior. Como uma afirmação que não pode ser provada, um postulado deve ser auto-evidente. Os elementos de Euclides são construídos sobre cinco postulados., Por mais de 2000 anos, o quinto postulado tem sido considerado menos intuitivo do que os outros postulados, e não suficientemente evidente. Muitas tentativas foram feitas para provar o quinto postulado usando os outros quatro postulados. Todas estas tentativas falharam. No século XIX ficou demonstrado que o quinto postulado é independente dos outros postulados. É possível construir uma teoria da geometria onde o quinto postulado não é verdadeiro. Tais geometrias são chamadas não-euclidianas. Além disso, pode ser demonstrado que as teorias não-euclidianas podem ser tão consistentes quanto a teoria Euclidiana., Uma teoria é consistente se não contiver qualquer contradição.
a afirmação inversa ao postulado paralelo, como indicado acima, é que não há linhas, ou pelo menos duas linhas “paralelas à linha dada através do ponto”. Pode ser mostrado que se há pelo menos duas linhas, há de fato infinitamente muitas linhas paralelas…”.
Se o postulado paralelo for substituído por:
Se o postulado paralelo for substituído por:
distâncias, ângulos e linhas

os teoremas nos elementos de Euclid são construídos sobre um número de postulados e um número de definições. A definição número 23 afirma que duas linhas são paralelas se nunca se encontrarem., Não há nada na definição que indique que a distância entre duas linhas paralelas é a mesma em toda parte. O postulado paralelo é aparentemente óbvio apenas se você assumir que linhas paralelas se parecem com trilhos de trem. Se você redefinir o que você quer dizer com uma linha, você pode ter que duas linhas paralelas ou convergem para o outro ou divergem um do outro.
na geometria não euclidiana, o conceito correspondente a uma linha é uma curva chamada geodésica. Na geometria não euclidiana, um caminho mais curto entre dois pontos é ao longo de uma linha geodésica ou não euclidiana.,
Todos os teoremas da geometria euclidiana que usam o quinto postulado, serão alterados quando reformular o postulado paralelo. Como exemplo, na geometria euclidiana a soma dos ângulos internos de um triângulo é 180°, na geometria não euclidiana este não é o caso.
Modelo de geometria elíptica
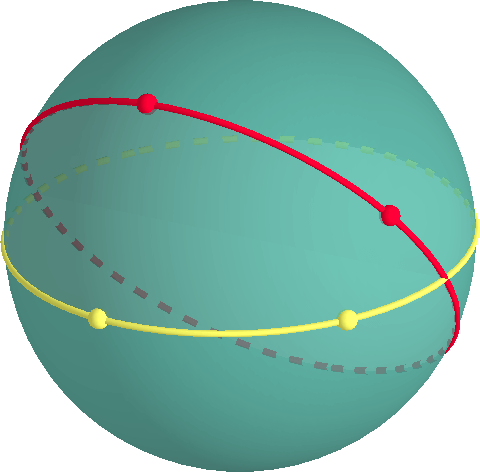
Uma maneira fácil de modelo de geometria elíptica é a de considerar a geometria da superfície de uma esfera. Um caminho mais curto entre dois pontos em asphere é ao longo de um chamado grande círculo., Um grande círculo é um círculo com o mesmo raio e o mesmo centro que a esfera. Um grande círculo é geodésico. se dois pontos estão diretamente opostos na esfera (como o polo norte e o polo sul), há infinitamente muitos caminhos mais curtos entre os pontos. Se os pontos não são antípodos, há apenas um caminho mais curto.
dois grandes círculos que não são os mesmos, devem Intersectar. Assim, não há linhas paralelas na superfície de uma esfera.
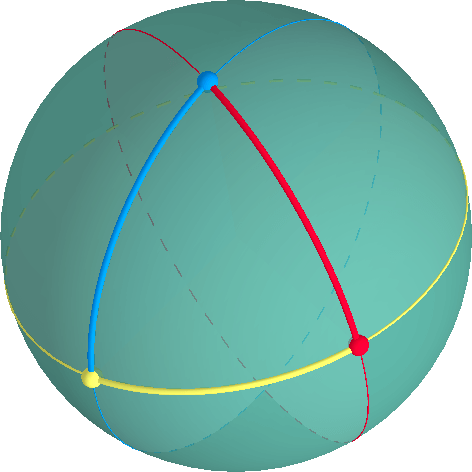
um triângulo é definido por três vértices e três arcos ao longo de grandes círculos através de cada par de vértices.,
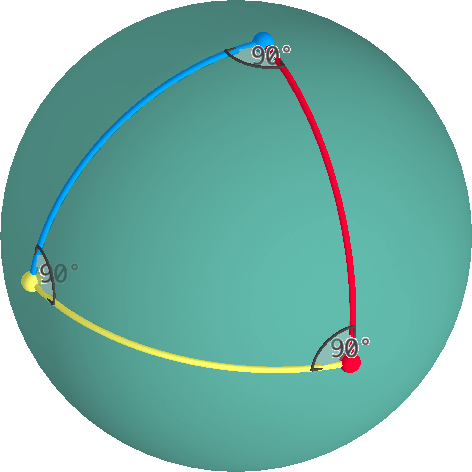
Um ângulo interior em um vértice de um triângulo pode ser medido no plano tangente através desse vértice. A soma dos ângulos internos de um triângulo elíptico é sempre > 180°.
geometria Hiperbólica usando o modelo de disco de Poincaré
O disco de Poincaré (em 2D) é um disco aberto, isto é, um conjunto de pontos, delimitada por um círculo, não incluindo o círculo., Ao usar o modelo de disco de Poincaré, apenas pontos no disco de Poincaré são considerados. O disco de Poincaré compõe o mundo inteiro. O limite do disco aberto é o círculo no infinito, \(C_\infty \).

mede-se um ângulo interior de um triângulo entre as correspondentes linhas tangentes., A soma dos ângulos internos é sempre < 180°. Se os vértices de um triângulo se movem para o círculo \(C_ \ infty \), a soma dos ângulos tende a 0. Os pontos que se encontram em \(C_ \ infty \) são chamados pontos ideais. O triângulo limitante como os vértices tendem ao infinito (\(c_\infty \)) é chamado de triângulo ideal. Um triângulo ideal tem soma de ângulo 0. Uma vez que os vértices de um triângulo ideal estão no infinito, o perímetro de um triângulo ideal é infinito. Além disso, pode ser mostrado que a área de um triângulo ideal é \(\pi\)., Assim, todos os triângulos na animação mais alta têm a mesma área hiperbólica.

geometria Hiperbólica usando o semi-plano de Poincaré modelo
Uma linha divide um plano em duas metades. Quando se utiliza o modelo de halfplane de Poincaré, apenas são considerados pontos em metade de um plano (não incluindo a linha).

exercícios
Exercício 1
para geometrias não euclidianas todos os postulados nos elementos de Euclides, exceto o postulado paralelo, devem ser verdadeiros. Se usar a geometria numa esfera para modelar a geometria elíptica, este não é o caso (dependendo de como interpreta o primeiro postulado). Use o guia para o postulado 1 para explicar por que a geometria em uma esfera, como explicado no texto, não é estritamente não-euclidiana.
Exercício 2
GeoGebra construção de geodésica elíptica.usando o GeoGebra mostre a janela gráfica 3D!, Você pode fazer esferas e planos usando comandos ou ferramentas. Para usar um comando Iniciar a digitação Sphere (ou Plane) e o GeoGebra irá mostrar-lhe várias alternativas para completar o código.um círculo sobre uma esfera pode ser construído intersectando a esfera com um plano. Você faz uma intersecção usando a ferramenta intersecta duas superfícies. Um grande círculo é construído escolhendo um plano apropriado para Intersectar a esfera com.,
Exercise 3
Measure an angle between two geodesics on a sphere using GeoGebra.
coloque três pontos \(A\), \(B\) E \(C\) numa esfera e construa dois geodésicos que formam o ângulo elíptico \ (\ângulo ABC \). O ângulo é medido usando pontos no plano através da tangente \(B\) à esfera. Construir o plano tangente. Construir dois pontos no plano que podem ser usados para medir o ângulo. Medir o ângulo e esconder todos os objectos auxiliares.,
animated gifs:
Ideal triangles on Ello.