Los números Indios discutidos en nuestro artículo los números Indios forman la base de los sistemas numéricos europeos que ahora se utilizan ampliamente. Sin embargo, no se transmitieron directamente de la India a Europa, sino que llegaron primero a los pueblos árabe/islámico y de ellos a Europa. Sin embargo, la historia de esta transmisión no es sencilla. Las partes oriental y occidental del mundo árabe vieron desarrollos separados de números indios con relativamente poca interacción entre los dos., Por la parte occidental del mundo árabe nos referimos a las regiones que comprenden principalmente el norte de África y España. La transmisión a Europa llegó a través de esta ruta árabe Occidental, entrando en Europa primero a través de España.hay otras complicaciones en la historia, sin embargo, porque no fue simplemente que los árabes se hicieron cargo del sistema numérico Indio. Más bien diferentes sistemas numéricos se utilizaron simultáneamente en el mundo árabe durante un largo período de tiempo., Por ejemplo, había al menos tres tipos diferentes de aritmética utilizados en los países árabes en el siglo XI: un sistema derivado de contar con los dedos con los números escritos enteramente en palabras, esta aritmética de cálculo de dedos era el sistema utilizado por la comunidad empresarial; el sistema sexagesimal con números denotados por letras del alfabeto árabe; y la aritmética de los números y fracciones indios con el sistema de valores decimales.la primera señal de que los números indios se movían hacia el oeste proviene de una fuente que es anterior al surgimiento de las naciones árabes., En 662 DC Severus Sebokht, un obispo nestoriano que vivía en Keneshra en el río Éufrates, escribió: –
omitiré toda discusión de la ciencia de los indios, … , de sus sutiles descubrimientos en astronomía, descubrimientos que son más ingeniosos que los de los griegos y los babilonios, y de sus valiosos métodos de cálculo que superan la descripción. Solo quiero decir que este cálculo se hace por medio de nueve signos., Si aquellos que creen, porque hablan griego, que han llegado a los límites de la ciencia, leerían los textos indios, se convencerían, incluso un poco tarde, de que hay otros que saben algo de valor.
este pasaje indica claramente que el conocimiento del sistema numérico indio era conocido en tierras que pronto se convertirían en parte del mundo árabe ya en el siglo VII. El pasaje en sí, por supuesto, ciertamente sugeriría que pocas personas en esa parte del mundo sabían algo del sistema., Severus Sebokht como obispo cristiano habría estado interesado en calcular la fecha de Pascua (un problema para las iglesias cristianas durante muchos cientos de años). Esto puede haberle animado a averiguar sobre las obras de astronomía de los indios y en estos, por supuesto, que encontraría la aritmética de los nueve símbolos.
Para el año 776 DC el imperio árabe estaba empezando a tomar forma y tenemos otra referencia a la transmisión de números Indios., Citamos de un trabajo de Al-Qifti Cronología de los eruditos escrito alrededor del final del siglo 12, pero citando fuentes mucho más antiguas: –
… una persona de la India se presentó ante el califa Al-Mansur en el año que estaba bien versado en el método siddhanta de cálculo relacionado con el movimiento de los cuerpos celestes, y tener formas de calcular ecuaciones basadas en el acorde medio calculado en grados medios … Todo esto está contenido en una obra … de la que afirmó haber tomado el medio acorde calculado para un minuto., Al-Mansur ordenó que este libro se tradujera al árabe, y que se escribiera un trabajo, basado en la traducción, para dar a los árabes una base sólida para calcular los movimientos de los planetas …
ahora en (donde se da una cita más larga) Ifrah intenta determinar a qué obra India se hace referencia. Llega a la conclusión de que lo más probable es que la obra fuera Brahmasphutasiddhanta (la apertura del universo) de Brahmagupta, escrita en 628., Independientemente de si Ifrah es correcto, ya que todos los textos indios después de Aryabhata I Aryabhatiya utiliza el sistema numérico indio de los nueve signos, sin duda a partir de este momento los árabes tenían una traducción al árabe de un texto escrito en el sistema numérico Indio.a menudo se afirma que el primer texto árabe escrito para explicar el sistema numérico Indio fue escrito por Al-Khwarizmi. Sin embargo, aquí hay dificultades que muchos autores tienden a ignorar., El texto árabe está perdido, pero una traducción latina del siglo XII, Algoritmi de numero Indorum gave dio lugar a la palabra algoritmo que deriva de su nombre en el título. Desafortunadamente, se sabe que la traducción latina ha cambiado mucho del texto original de Al-Khwarizmi (del cual incluso se desconoce el título). El texto latino ciertamente describe el sistema indio de valores de lugar de los números basados en 1, 2, 3, 4, 5, 6, 7, 8, 9, y 0. El primer uso del cero como un lugar titular en la notación base posicional es considerado por algunos como debido a al-Khwarizmi en este trabajo., La dificultad que surge es que al-Baghdadi se refiere al original árabe que, contrariamente a lo que se pensaba originalmente, parece no ser un trabajo sobre números indios, sino más bien un trabajo sobre métodos de conteo de dedos. Esto queda claro a partir de las referencias de Al-Baghdadi a la obra perdida. Sin embargo, las numerosas referencias al libro de Al-Khwarizmi sobre los nueve símbolos indios deben significar que él escribió tal trabajo. Un cierto grado de misterio aún permanece.
Al principio los métodos indios fueron utilizados por los árabes con una tabla de polvo., De hecho, en la parte occidental del mundo árabe los números indios llegaron a ser conocidos como Guba (o Gubar o Ghubar) números de la palabra árabe que significa «polvo». Se utilizó un tablero de polvo porque los métodos aritméticos requerían el movimiento de los números en el cálculo y frotando algunos de ellos a medida que avanzaba el cálculo. El tablero de polvo permitió esto de la misma manera que se puede usar una pizarra, tiza y una goma de borrar de pizarra., Cualquier estudiante que haya asistido a conferencias donde el profesor cambia continuamente y reemplaza partes de las matemáticas a medida que avanza la demostración comprenderá la desventaja del tablero de polvo!a mediados del siglo x al-Uqlidisi escribió Kitab Al-fusul fi al-hisab al-Hindi which que es el libro más antiguo que se conserva que presenta el sistema indio., En él al-Uqlidisi argumenta que el sistema es de valor práctico: –
la mayoría de los aritméticos están obligados a usarlo en su trabajo: ya que es fácil e inmediato, requiere poca memorización, proporciona respuestas rápidas, exige poco pensamiento … Por lo tanto, decimos que es una ciencia y una práctica que requiere una herramienta, como un escritor, un artesano, un caballero necesita conducir sus asuntos; ya que si el artesano tiene dificultad en encontrar lo que necesita para su oficio, nunca tendrá éxito; para captarlo no hay dificultad, imposibilidad o preparación.,
en la cuarta parte de este libro al-Uqlidisi mostró cómo modificar los métodos de cálculo con símbolos indios, que habían requerido un tablero de polvo, a métodos que podrían llevarse a cabo con pluma y papel. Ciertamente, el hecho de que el sistema indio requiriera un tablero de polvo había sido uno de los principales obstáculos para su aceptación., Por ejemplo, As-Suli, después de elogiar el sistema indio por su gran simplicidad, escribió en la primera mitad del siglo X:-
los escribas oficiales, sin embargo, evitan usar porque requiere equipo y consideran que un sistema que solo requiere los miembros del cuerpo es más seguro y más adecuado a la dignidad de un líder.
el trabajo de Al-Uqlidisi es por lo tanto importante en el intento de eliminar uno de los obstáculos para la aceptación de los nueve símbolos Indios., También es históricamente importante, ya que es el texto más antiguo conocido que ofrece un tratamiento directo de las fracciones decimales.a pesar de que muchos eruditos encontraron que el cálculo con símbolos Indios era útil en su trabajo, la comunidad empresarial continuó usando su aritmética de dedos durante todo el siglo X. Abu’l-Wafa, que era un experto en el uso de números indios, sin embargo, escribió un texto sobre cómo utilizar la aritmética de cálculo de dedos, ya que este era el sistema utilizado por la comunidad empresarial y el material de enseñanza dirigido a estas personas tenía que ser escrito utilizando el sistema apropiado., Vamos a dar un poco de información sobre los números de letras árabes que están contenidos en la obra de Abu’l-Wafa.
los números fueron representados por letras pero no en el orden del diccionario. El sistema era conocido como huruf Al jumal que significaba «letras para calcular» y también a veces como abjad que es solo los primeros cuatro números (1 = a, 2 = b, j = 3, d = 4). Los números del 1 al 9 fueron representados por letras, luego los números 10, 20, 30, …, 90 por las siguientes nueve letras (10 = y, 20 = k, 30 = l, 40 = m, …), entonces 100, 200, 300, … , 900 por las letras siguientes (100 = q, 200 = r, 300 = sh, 400 = ta, …,). Había 28 letras árabes y así quedó una que se utilizó para representar 1000.los astrónomos árabes utilizaron una versión base 60 del sistema de letras árabes. Aunque el árabe se escribe de derecha a izquierda, vamos a dar un ejemplo de escritura en el estilo de izquierda a derecha que utilizamos en la escritura en inglés. Un número, digamos 43° 21 ’14», habría sido escrito como» mj ka yd «en esta versión base 60 de las letras» abjad » para calcular.un contemporáneo de Al-Baghdadi, escrito a principios del siglo XI, fue ibn Sina (más conocido en Occidente como Avicena)., Sabemos muchos detalles de su vida porque escribió una autobiografía. Ciertamente ibn Sina era un niño notable, con una memoria y una capacidad de aprender que asombró a los eruditos que se reunieron en la casa de su padre. Un grupo de eruditos de Egipto llegó a la casa de su padre en aproximadamente 997 cuando ibn Sina tenía diez años y le enseñaron aritmética India. También cuenta que un vendedor de verduras le enseñó cálculo indio y álgebra., Todo esto muestra que a principios del siglo XI el cálculo con los símbolos Indios estaba bastante extendido y, bastante significativamente, era conocido por un comerciante de verduras.
Lo de los números en sí. Hemos visto en el artículo Indian numerals que la forma de los números mismos varió en diferentes regiones y cambió con el tiempo. Exactamente lo mismo sucedió en el mundo árabe.
Aquí está un ejemplo de una forma temprana de números indios que se utiliza en la parte oriental del imperio árabe., Proviene de una obra de al-Sijzi, no un trabajo original de él, sino más bien el trabajo de otro matemático que al-Sijzi copió en Shiraz y fechado su copia 969.
Los números del Tratado de 969 de Al-Sizji
los números habían cambiado su forma algo 100 años más tarde cuando se hizo esta copia de uno de los textos astronómicos de Al-Biruni. Aquí están los números tal como aparecen en una copia de 1082.,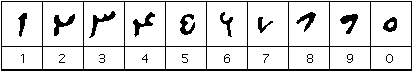
Los números del Tratado de Al-Biruni copiado en 1082
De hecho, una mirada más cercana mostrará que entre 969 y 1082 el mayor cambio en los números fue el hecho de que el 2 y el 3 se han girado a través de 90°. Hay una razón para este cambio que se produjo debido a la forma en que escribieron los escribas, porque escribieron en un pergamino que enrollaron de derecha a izquierda a través de sus cuerpos mientras se sentaban con las piernas cruzadas. Los escribas, por lo tanto, en lugar de escribir de derecha a izquierda (la forma estándar en que se escribía el árabe) escribieron en líneas de arriba a abajo., El guion se giraba cuando se leía el pergamino y los caracteres cuando se encontraban en la orientación correcta.
Aquí hay un ejemplo de cómo se escribió el texto
quizás porque los escribas no tenían mucha experiencia en escribir números Indios, escribieron 2 y 3 de la manera correcta en lugar de escribirlos rotados 90° para que aparecieran correctamente cuando se giraba el rollo para ser leído.,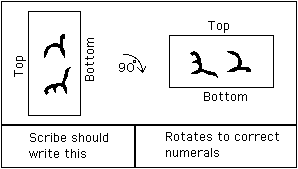
Aquí está un ejemplo de lo que el escriba debe escribir
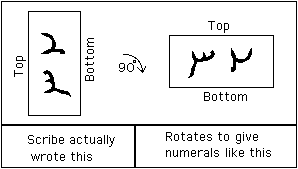
y aquí está lo que el escriba realmente escribió
la forma de los números en el oeste del imperio árabe parece más familiar para aquellos que usan números europeos hoy en día, lo que no es sorprendente dado que es a partir de estos números que el sistema numérico Indio llega a Europa.,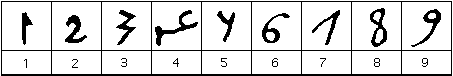
La forma de los números de Al-Banna al-Marrakushi
dio esta forma de los números en su libro de aritmética práctica escrito a principios del siglo XIV. Vivió la mayor parte de su vida en Marruecos, que estaba en estrecho contacto con Al-Andalus, o Andalucía, que era la región controlada por los árabes en el sur de España.
el primer ejemplo sobreviviente de los números indios en un documento en Europa fue, sin embargo, mucho antes de la época de Al-Banna. Los números aparecen en el Códice Vigilanus copiado por un monje en España en 976., Sin embargo, la parte principal de Europa no estaba preparada en este momento para aceptar nuevas ideas de ningún tipo. La aceptación fue lenta, incluso en el siglo XV, cuando las matemáticas europeas comenzaron su rápido desarrollo que continúa hoy en día. En este artículo no examinaremos las numerosas contribuciones para llevar el sistema numérico Indio a Europa, pero terminaremos con un solo ejemplo que, sin embargo, es muy importante., Fibonacci escribe en su famoso libro Liber abaci published publicado en Pisa en 1202: –
cuando mi padre, que había sido nombrado por su país como notario público en la aduana de Bugia actuando para los comerciantes Pisanos que iban allí, estaba a cargo, me convocó a él cuando todavía era un niño, y teniendo un ojo para la utilidad y la conveniencia futura, deseó que me quedara allí y recibir instrucción en la escuela de contabilidad., Allí, cuando me habían introducido en el arte de los nueve símbolos de los indios a través de la enseñanza notable, el conocimiento del arte muy pronto me complació por encima de todo lo demás y llegué a comprenderlo, para todo lo que fue estudiado por el arte en Egipto, Siria, Grecia, Sicilia y Provenza, en todas sus diversas formas.