Geometria non euclidea

Il postulato parallelo

Il quinto postulato negli elementi di Euclide può essere riformulato come

Il postulato non è vero in 3D ma in 2D sembra essere una dichiarazione valida., Considerando l’importanza dei postulatituttavia, una dichiarazione apparentemente valida non è abbastanza buona.

Un postulato (o assioma) è una dichiarazione che funge da punto di partenza per una teoria. Poiché un postulato è un punto di partenza, non può essere provato usando il risultato precedente. Come affermazione che non può essere provata, un postulato dovrebbe essere evidente. Gli elementi di Euclide è costruito su cinque postulati., Per oltre 2000 anni il quinto postulato è stato considerato meno intuitivo degli altri postulati e non sufficientemente evidente. Molti tentativi sono stati fatti per dimostrare il quinto postulato utilizzando gli altri quattro postulati. Tutti questi tentativi sono falliti. Nel 19 ° secolo è stato dimostrato che il quinto postulato è indipendente dagli altri postulati. È possibile costruire una teoria della geometria in cui il quinto postulato non è vero. Tali geometrie sono chiamate non euclidee. Inoltre, si può dimostrare che le teorie non euclidee possono essere coerenti quanto la teoria euclidea., Una teoria è coerente se non contiene alcuna contraddizione.

L’istruzione inversa al postulato parallelo, come detto sopra, è che non ci sono linee, o almeno due linee “parallele alla linea data attraverso il punto”. Si può dimostrare che se ci sono almeno due linee, ci sono infatti infinitamente molte linee “parallele a…”.

Se il postulato parallelo è sostituito da:

si ottiene una geometria ellittica.,

Se il postulato parallelo è sostituito da:

si ottiene una geometria iperbolica.

Distanze, angoli e linee

I teoremi negli Elementi di Euclide sono costruiti su un numero di postulati e un numero di definizioni. Definizione numero 23 afferma che due linee sono parallele se non si incontrano mai., Non c’è nulla nella definizione che indichi che la distanza tra due linee parallele sia la stessa ovunque. Il postulato parallelo è apparentemente ovvio solo se si assume che le linee parallele assomiglino ai binari della ferrovia. Se ridefinisci cosa intendi con una linea, potresti avere che due linee parallele convergono l’una verso l’altra o divergono l’una dall’altra.

Nella geometria non euclidea, il concetto corrispondente a una linea è una curva chiamata geodetica. Nella geometria non euclidea un percorso più breve tra due punti è lungo una tale linea geodetica, o “linea non euclidea”.,

Tutti i teoremi della geometria euclidea che usano il quinto postulato verranno modificati quando si riformula il postulato parallelo. Ad esempio; nella geometria euclidea la somma degli angoli interni di un triangolo è di 180°, nella geometria non euclidea questo non è il caso.

Modello di geometria ellittica

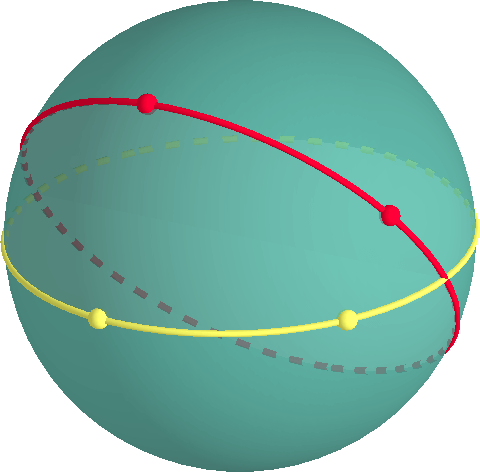
Un modo semplice per modellare la geometria ellittica è considerare la geometria sulla superficie di una sfera. Un percorso più breve tra due punti su asfere è lungo un cosiddetto grande cerchio., Un grande cerchio è un cerchio avente lo stesso raggio e lo stesso centro della sfera. Un grande cerchio è una geodetica.

Se due punti sono direttamente uno di fronte all’altro sulla sfera (come il polo nord e il polo sud) ci sono infiniti percorsi più brevi tra i punti. Se i punti non lo sonoantipodi, c’è solo un percorso più breve.

Due grandi cerchi che non sono gli stessi, devono intersecarsi. Quindi, non ci sono linee parallele sulla superficie di una sfera.

Un triangolo è definito da tre vertici e tre archi lungo grandi cerchi attraverso ogni coppia di vertici.,

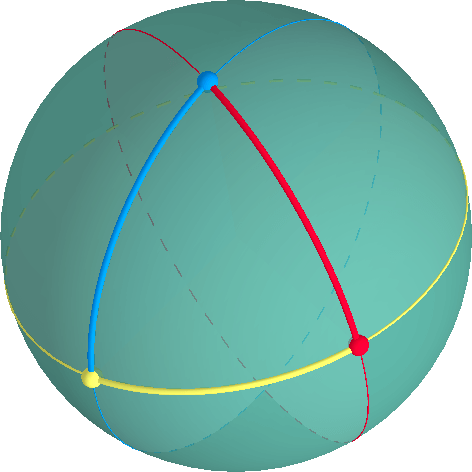
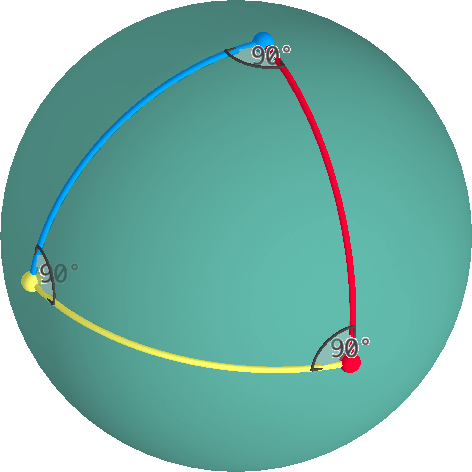
Un angolo interno ad un vertice di un triangolo può essere misurato sul piano tangente attraverso quel vertice. La somma degli angoli interni di un triangolo ellittico è sempre > 180°.

geometria Iperbolica, utilizzando il modello del disco di Poincaré

Il disco di Poincaré (in 2D) è un open disc, cioè un insieme di punti delimitata da un cerchio, che non comprese il cerchio., Quando si utilizza il modello di disco di Poincaré, vengono considerati solo i punti nel disco di Poincaré. Il disco Poincaré costituisce il mondo intero. Il limite del disco aperto è il cerchio all’infinito, \(C_ \ infty\).

Un angolo interno di un triangolo viene misurato tra le corrispondenti linee tangenti., La somma degli angoli interni è sempre < 180°. Se i vertici di un triangolo si muovono verso il cerchio \ (C_ \ infty\), la somma dell’angolo tende a 0. I punti che si trovano a \(C_ \ infty\) sono chiamati punti ideali. Il triangolo limitante come i vertici tendono all’infinito (\(C_ \ infty\)) è chiamato un triangolo ideale. Un triangolo ideale ha somma angolo 0. Poiché i vertici di un triangolo ideale si trovano all’infinito, il perimetro di un triangolo ideale è infinito. Inoltre, si può dimostrare che l’area di un triangolo ideale è \(\pi\)., Quindi, tutti i triangoli nell’animazione più in alto hanno la stessa area iperbolica.

Geometria iperbolica utilizzando il modello halfplane di Poincaré

Una linea divide un piano in due metà. Quando si utilizza il modello Poincaré halfplane, vengono considerati solo i punti a metà di un piano (esclusa la linea).

Esercizi

Esercizio 1

Per geometrie non euclidee tutti i postulati negli Elementi di Euclide tranne il postulato parallelo dovrebbero essere veri. Se si utilizza la geometria su una sfera per modellare la geometria ellittica, questo non è il caso (a seconda di come si interpreta il primo postulato). Usa la Guida per il postulato 1 per spiegare perché la geometria su una sfera, come spiegato nel testo, non è strettamente non euclidea.

Esercizio 2

GeoGebra costruzione di geodetica ellittica.

Utilizzando GeoGebra mostra la finestra Grafica 3D!, Puoi creare sfere e piani usando comandi o strumenti. Per usare un comando inizia a digitare Sphere (o Plane) e GeoGebra ti mostrerà varie alternative per completare il codice.

Un cerchio su una sfera può essere costruito intersecando la sfera con un piano. Si effettua un’intersezione utilizzando lo strumento Interseca due superfici. Un grande cerchio è costruito scegliendo un piano appropriato per intersecare la sfera con.,

Esercizio 3

Misurare un angolo tra due geodetiche su una sfera usando GeoGebra.

Metti tre punti \(A\), \(B\) e \(C\) su una sfera e costruisci due geodetiche che formano l’angolo ellittico \( \angle ABC \). L’angolo viene misurato utilizzando punti sul piano attraverso\ (B\) tangente alla sfera. Costruisci il piano tangente. Costruire due punti sul piano che può essere utilizzato per misurare l’angolo. Misurare l’angolo e nascondere tutti gli oggetti ausiliari.,

animated gifs:

Ideal triangles on Ello.